摘要: 如图.已知△ABC是边长为1的正三角形.M.N分别是 边AB.AC上的点.线段MN经过△ABC的中心G. 设ÐMGA=a() (1) 试将△AGM.△AGN的面积(分别记为S1与S2) 表示为a的函数 (2) 求y=的最大值与最小值 解:(1)因为G是边长为1的正三角形ABC的中心. 所以 AG=.ÐMAG=. 由正弦定理,得 则S1=GM·GA·sina=, 同理可求得S2=. (2)y== =72(3+cot2a)因为.所以当a=或a=时.y取得最大值ymax=240 当a=时.y取得最小值ymin=216
网址:http://m.1010jiajiao.com/timu3_id_4468792[举报]
(本小题满分12分)
如图,已知圆锥的轴截面ABC是边长为 的正三角形,O是底面圆心.
的正三角形,O是底面圆心.

(1)求圆锥的表面积;
(2)经过圆锥的高 的中点
的中点 作平行于圆锥底面的截面,求截得的圆台的体积.
作平行于圆锥底面的截面,求截得的圆台的体积.
查看习题详情和答案>>
 的正三角形,O是底面圆心.
的正三角形,O是底面圆心.
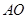 的中点
的中点 作平行于圆锥底面的截面,求截得的圆台的体积.
作平行于圆锥底面的截面,求截得的圆台的体积. 的正三角形,O是底面圆心.
的正三角形,O是底面圆心.
 的中点
的中点 作平行于圆锥底面的截面,求截得的圆台的体积.
作平行于圆锥底面的截面,求截得的圆台的体积.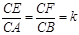 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 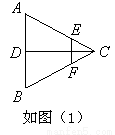
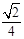 ,求k的值.
,求k的值. 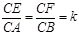 ,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2).
,现将△ABC沿CD翻折成直二面角A-DC-B,如图(2). 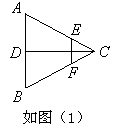
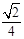 ,求k的值.
,求k的值.