摘要： 已知函数f(x)＝x3+ax2+bx+c在x＝-与x＝1时都取得极值 (1) 求a.b的值与函数f(x)的单调区间 (2) 若对xÎ<c2恒成立.求c的取值范围. 解:(1)f(x)＝x3+ax2+bx+c.f¢(x)＝3x2+2ax+b 由f¢()＝.f¢(1)＝3+2a+b＝0得 a＝.b＝-2 f¢(x)＝3x2-x-2＝.函数f(x)的单调区间如下表: x (-¥.-) - (-.1) 1 f¢(x) + 0 - 0 + f(x) 极大值 ¯ 极小值 所以函数f(x)的递增区间是(-¥.-)与 递减区间是(-.1) (2)f(x)＝x3-x2-2x+c.xÎ.当x＝-时.f(x)＝+c 为极大值.而f(2)＝2+c.则f(2)＝2+c为最大值. 要使f(x)<c2恒成立.只需c2>f(2)＝2+c 解得c<-1或c>2
网址：http://m.1010jiajiao.com/timu3_id_4468790[举报]
(本小题满分12分)已知函数f(x)＝x3＋x2－2.
(1)设{an}是正数组成的数列，前n项和为Sn，其中a1＝3.若点(an，an＋12－2an＋1)(n∈N*)在函数y＝f′(x)的图象上，求证：点(n，Sn)也在y＝f′(x)的图象上；
(2)求函数f(x)在区间(a－1，a)内的极值．
查看习题详情和答案>>
(本小题满分12分)已知函数f(x)＝x3＋x2－2.
(1)设{an}是正数组成的数列，前n项和为Sn，其中a1＝3.若点(an，an＋12－2an＋1)(n∈N*)在函数y＝f′(x)的图象上，求证：点(n，Sn)也在y＝f′(x)的图象上；
(2)求函数f(x)在区间(a－1，a)内的极值．
(1)设{an}是正数组成的数列，前n项和为Sn，其中a1＝3.若点(an，an＋12－2an＋1)(n∈N*)在函数y＝f′(x)的图象上，求证：点(n，Sn)也在y＝f′(x)的图象上；
(2)求函数f(x)在区间(a－1，a)内的极值．
（本小题满分12分）已知函数f(x)＝x3－ax2－3x.
(1)若f(x)在x∈[1，＋∞)上是增函数，求实数a的取值范围；
(2)若x＝3是f(x)的极值点，求f(x)在x∈[1，a]上的最小值和最大值．
查看习题详情和答案>>
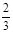与x＝1时都取得极值.