题目内容
(本小题满分12分)已知函数f(x)=x3-ax2-3x.
(1)若f(x)在x∈[1,+∞)上是增函数,求实数a的取值范围;
(2)若x=3是f(x)的极值点,求f(x)在x∈[1,a]上的最小值和最大值.
【答案】
(1) a≤0(2) f(x)max=-6,f(x)min=-18.
【解析】
试题分析:(1)对f(x)求导,得f′(x)=3x2-2ax-3. ………………1分
由f′(x)>0(x≥1),得a<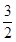 (x-
(x- ).………………2分
).………………2分
记t(x)=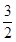 (x-
(x- ),
),
当x≥1时,t(x)是增函数,∴t(x)min=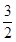 (1-1)=0. ………………3分
(1-1)=0. ………………3分
∴a<0,又∵a=0时也符合题意,故a≤0. ………………4分
(2)由题意,得f′(3)=0,即27-6a-3=0,∴a=4,………………6分
∴f(x)=x3-4x2-3x,f′(x)=3x2-8x-3.
令f′(x)=0,得x1=-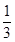 ,x2=3. ………………8分
,x2=3. ………………8分
当x变化时,f′(x)、f(x)的变化情况如下表:
|
x |
(-∞,- |
- |
(- |
3 |
(3,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
|
极大值 |
? |
极小值 |
|
∴当x∈(-∞,-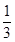 ]与[3,+∞)时,f(x)是增函数;当x∈[-
]与[3,+∞)时,f(x)是增函数;当x∈[-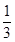 ,3]时,f(x)是减函数.
,3]时,f(x)是减函数.
于是,当x∈[1,4]时,有极小值f(3)=-18;………………10分
而f(1)=-6,f(4)=-12,
∴f(x)max=f(1)=-6,f(x)min=-18. ………………12分
考点:利用导数判定函数单调性,求函数的最值
点评:解(1)过程中将不等式恒成立问题转化为求函数最值问题

练习册系列答案
相关题目
 ?
?