摘要:17. 在梯形ABCD中.AB=BC=2.AD=4.∠CBA=∠BAD=90°.沿对角线AC将ΔABC折起.使点B在平面ACD内的射影O恰在AC上 (1)求证:AB⊥平面BCD, (2)求异面直线BC与AD所成的角.
网址:http://m.1010jiajiao.com/timu3_id_4468601[举报]
 (本题满分14分)
(本题满分14分)
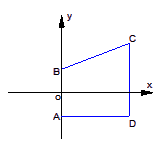
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
(3)设轨迹E与直线![]() 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
查看习题详情和答案>>(本题满分14分)
如图3,在四棱锥P—ABCD中,底面为直角梯形,AD//BC,ÐBAD=90°,PA^底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
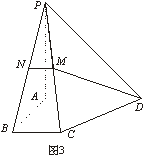 (1)求证:PB^DM;
(1)求证:PB^DM;
(2)求BD与平面ADMN所成角的大小;
(3)求二面角B—PC—D的大小.
查看习题详情和答案>>(本题满分14分)
如图3,在四棱锥P—ABCD中,底面为直角梯形,AD//BC,ÐBAD=90°,PA^底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
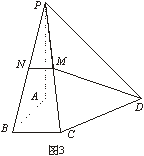 (1)求证:PB^DM;
(1)求证:PB^DM;
(2)求BD与平面ADMN所成角的大小;
(3)求二面角B—PC—D的大小.
查看习题详情和答案>>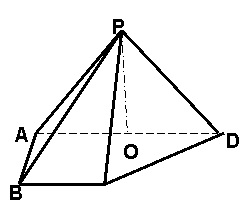 (Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅱ)求异面直线PB与CD所成角的余弦值;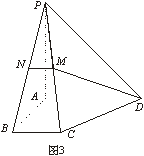 (1)求证:PB^DM;
(1)求证:PB^DM;