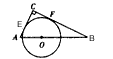
摘要:已知RtΔABC中.∠C=90.BC=a.AC=b.以斜边AB上一点O为圆心.作⊙O使⊙O与直角边AC.BC都相切.则⊙O的半径r为( ) A. B. C. D.
网址:http://m.1010jiajiao.com/timu3_id_446857[举报]
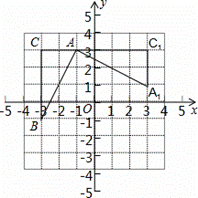
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
【小题1】请写出旋转中心的坐标是 ,旋转角是 度;
【小题2】以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
【小题3】设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.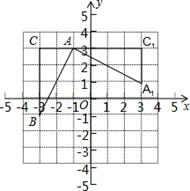
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
小题1:请写出旋转中心的坐标是 ,旋转角是 度;
小题2:以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
小题3:设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.
小题1:请写出旋转中心的坐标是 ,旋转角是 度;
小题2:以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
小题3:设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.

如图,在平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
(1)请写出旋转中心的坐标是 ,旋转角是 度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形;
(3)设Rt△ABC两直角边BC=a、AC=b、斜边AB=c,利用变换前后所形成的图案证明勾股定理.