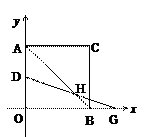摘要： 在平面直角坐标系中.A点坐标为 . C点坐标为 . (1) 如图1:若直线AB∥OC .直线AB上有一动点 P .若△POC为等腰三角形时.求P点坐标. (2) 如图2 :若直线AB与OC不平行.过点A的直线y= ―x+4 上是否存在点P.使 ∠OPC=900 .若存在这样的点P.求出它的坐标.若不存在.请简要说明理由. (3)若点P在直线y=kx+4上移动.且只存在唯一一个点P . 使∠OPC=900 . 试求出k的值. 初三数学第二学期阶段性质量检测试卷答题卷
网址：http://m.1010jiajiao.com/timu3_id_446843[举报]
（本题14分）在平面直角坐标系中，已知抛物线经过
、
、
三点．
⑴求抛物线的解析式；
⑵若点M为第三象限内抛物线上一动点，点M的横坐标为m,△AMB的面积为S．求S关于m的函数关系式，并求出S的最大值；
⑶若点P是抛物线上的动点，点Q是直线
上的动点，判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
查看习题详情和答案>>
（本题满分为14分）平面直角坐标系中，正方形AOBC如图所示，点C的坐标为（a，a），其中a使得式子
有意义，反比例函数
的图象经过点C.
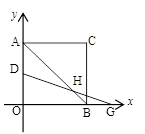
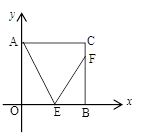
（1）求反比例函数解析式.
（2）若有一点D自A向O运动，且满足AD2=OD·AO，求此时D点坐标.
（3）若点D在AO上、G为OB的延长线上的点，AD=BG，连接AB交DG于点H，写出AB－2HB与AD之间的数量关系（直接写出不需证明）.
（4）如图，点E为正方形AOBC的OB边一点，点F为BC上一点且∠CAE=∠FEA=60°，求直线EF的解析式.
查看习题详情和答案>>
（本题满分为14分）平面直角坐标系中，正方形AOBC如图所示，点C的坐标为（a，a），其中a使得式子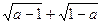
有意义，反比例函数
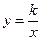的图象经过点C.
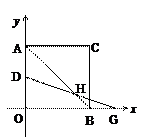
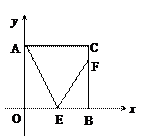
（1）求反比例函数解析式.
（2）若有一点D自A向O运动，且满足AD2=OD·AO，求此时D点坐标.
（3）若点D在AO上、G为OB的延长线上的点，AD=BG，连接AB交DG于点H，写出AB－2HB与AD之间的数量关系（直接写出不需证明）.
（4）如图，点E为正方形AOBC的OB边一点，点F为BC上一点且∠CAE=∠FEA=60°，求直线EF的解析式. 查看习题详情和答案>>
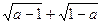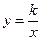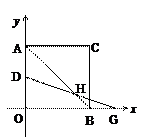
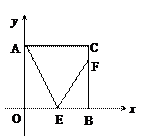
有意义，反比例函数的图象经过点C.（1）求反比例函数解析式.
（2）若有一点D自A向O运动，且满足AD2=OD·AO，求此时D点坐标.
（3）若点D在AO上、G为OB的延长线上的点，AD=BG，连接AB交DG于点H，写出AB－2HB与AD之间的数量关系（直接写出不需证明）.
（4）如图，点E为正方形AOBC的OB边一点，点F为BC上一点且∠CAE=∠FEA=60°，求直线EF的解析式. 查看习题详情和答案>>
、
、
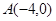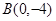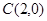三点．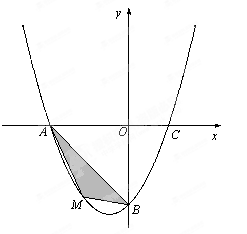
上的动点，判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．
有意义，反比例函数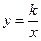
的图象经过点C.
