摘要：18．已知数列{an}中.a1=2..bn是方程(an+1)2x2-2(an+1)x+1=0的根, (1)探索数列{an}的通项公式并说明理由, (2)设函数.求的最小值. 解: 19．如图.正三棱柱ABC-A1B1C1的底面边长的3.侧棱AA1=D是CB延长线上一点.且BD=BC. (Ⅰ)求证:直线BC1//平面AB1D, (Ⅱ)求二面角B1-AD-B的大小, (Ⅲ)求三棱锥C1-ABB1的体积. (Ⅰ)证明:CD//C1B1.又BD=BC=B1C1. ∴ 四边形BDB1C1是平行四边形. ∴BC1//DB1. 又DB1平面AB1D.BC1平面AB1D. ∴直线BC1//平面AB1D. (Ⅱ)解:过B作BE⊥AD于E.连结EB1. ∵B1B⊥平面ABD.∴B1E⊥AD . ∴∠B1EB是二面角B1-AD-B的平面角. ∵BD=BC=AB. ∴E是AD的中点. 在Rt△B1BE中. ∴∠B1EB=60°.即二面角B1-AD-B的大小为60° (Ⅲ)解法一:过A作AF⊥BC于F.∵B1B⊥平面ABC.∴平面ABC⊥平面BB1C1C. ∴AF⊥平面BB1C1C.且AF= 即三棱锥C1-ABB1的体积为 解法二:在三棱柱ABC-A1B1C1中. 即三棱锥C1-ABB1的体积为
网址：http://m.1010jiajiao.com/timu3_id_4466156[举报]
已知数列{an}中，a1=
，点（n，2an+1-an）在直线y=x上，n∈N*．
（1）令bn=an+1-an-1，证明：{bn}为等比数列；
（2）求数列{an}的通项公式；
（3）设Sn、Tn分别为数列{an}、{bn}的前n项和，是否存在实数λ，使得数列{
}为等差数列？若存在，求出λ的值，并给出证明；若不存在，说明理由．
查看习题详情和答案>>
| 1 |
| 2 |
（1）令bn=an+1-an-1，证明：{bn}为等比数列；
（2）求数列{an}的通项公式；
（3）设Sn、Tn分别为数列{an}、{bn}的前n项和，是否存在实数λ，使得数列{
| Sn+λTn |
| n |
已知数列{an}中，a1=0，an+1=
，n∈N*．
（1）求证：{
}是等差数列；并求数列{an}的通项公式；
（2）假设对于任意的正整数m、n，都有|bn-bm|＜ω，则称该数列为“ω域收敛数列”．试判断：数列bn=an•(-
)n，n∈N*是否为一个“
域收敛数列”，请说明你的理由．
查看习题详情和答案>>
| 1 |
| 2-an |
（1）求证：{
| 1 |
| an-1 |
（2）假设对于任意的正整数m、n，都有|bn-bm|＜ω，则称该数列为“ω域收敛数列”．试判断：数列bn=an•(-
| 4 |
| 5 |
| 2 |
| 3 |
已知数列{an}中，a1=
，点（n，2an+1-an）在直线y=x上，n∈N*．
（1）令bn=an+1-an-1，证明：{bn}为等比数列；
（2）求数列{an}的通项公式；
（3）设Sn、Tn分别为数列{an}、{bn}的前n项和，是否存在实数λ，使得数列{
}为等差数列？若存在，求出λ的值，并给出证明；若不存在，说明理由．
查看习题详情和答案>>
| 1 |
| 2 |
（1）令bn=an+1-an-1，证明：{bn}为等比数列；
（2）求数列{an}的通项公式；
（3）设Sn、Tn分别为数列{an}、{bn}的前n项和，是否存在实数λ，使得数列{
| Sn+λTn |
| n |
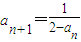，n∈N*．
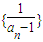是等差数列；并求数列{an}的通项公式；
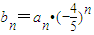，n∈N*是否为一个“
域收敛数列”，请说明你的理由．