题目内容
已知数列{an}中,a1=0,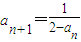 ,n∈N*.
,n∈N*.(1)求证:
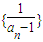 是等差数列;并求数列{an}的通项公式;
是等差数列;并求数列{an}的通项公式;(2)假设对于任意的正整数m、n,都有|bn-bm|<ω,则称该数列为“ω域收敛数列”.试判断:数列
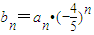 ,n∈N*是否为一个“
,n∈N*是否为一个“ 域收敛数列”,请说明你的理由.
域收敛数列”,请说明你的理由.
【答案】分析:(1)根据题中所给出的等式,求数列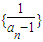 的相邻两项的差,并将这个差进行化简,最终得出这个差等于-1,得出数列
的相邻两项的差,并将这个差进行化简,最终得出这个差等于-1,得出数列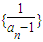 是公差为-1的等差数列,则不难通过数列
是公差为-1的等差数列,则不难通过数列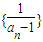 求出数列{an}的通项公式;
求出数列{an}的通项公式;
(2)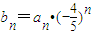 ,说明数列{bn}的奇数项为负数,偶数项为正数.通过作差:|bn+1|-|bn|,化简得|bn+1|-|bn|=
,说明数列{bn}的奇数项为负数,偶数项为正数.通过作差:|bn+1|-|bn|,化简得|bn+1|-|bn|=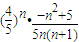 ,讨论得当n=3时,|b3|是数列{|bn|}的最大项,但是b3<0,说明b3是{bn}最小的项,而在正数项中,绝对第二大的项可能是b2或b4,通过作差比较可得b2是数列{bn}的最大项.在此基础之上不难用定义:对于任意的正整数m、n,都有|bn-bm|<ω,则称该数列为“ω域收敛数列”,证明数列{bn}是一个“
,讨论得当n=3时,|b3|是数列{|bn|}的最大项,但是b3<0,说明b3是{bn}最小的项,而在正数项中,绝对第二大的项可能是b2或b4,通过作差比较可得b2是数列{bn}的最大项.在此基础之上不难用定义:对于任意的正整数m、n,都有|bn-bm|<ω,则称该数列为“ω域收敛数列”,证明数列{bn}是一个“ 域收敛数列”了.
域收敛数列”了.
解答:证:(1)因为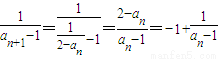 ,
,
所以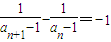 ,n∈N*;
,n∈N*;
故 是等差数列.
是等差数列.
由此可得,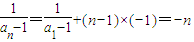 ,
,
所以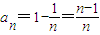 ,n∈N*.
,n∈N*.
(2)由条件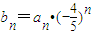 ,
,
可知当n=2k,bn>0;当n=2k-1时,bn≤0,k∈N*.
令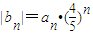 ,则
,则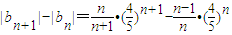 =
=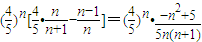 .
.
∴当-n2+5>0⇒n≤2时,|bn+1|>|bn|;
同理可得,当-n2+5<0⇒n≥3时,|bn+1|<|bn|;
即数列{|bn|}在n=1,2,3时递增;n≥4时,递减;
即|b3|是数列{|bn|}的最大项.
然而,因为{bn}的奇数项均为-|bn|,故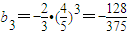 为数列{bn}的最小项;
为数列{bn}的最小项;
而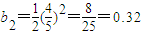 ,
,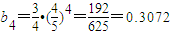 ,
,
所以b2>b4,故b2是数列{bn}的最大项.
∴对任意的正整数m、n,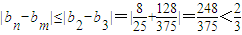 ,
,
∴数列 ,n∈N*是一个“
,n∈N*是一个“ 域收敛数列”.
域收敛数列”.
点评:本题是一道由一个数列为基础,同时考查了函数不等式的相关知识,属于难题.着重考查数列的性质和应用,解题时要注意认真审题,仔细计算.
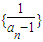 的相邻两项的差,并将这个差进行化简,最终得出这个差等于-1,得出数列
的相邻两项的差,并将这个差进行化简,最终得出这个差等于-1,得出数列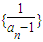 是公差为-1的等差数列,则不难通过数列
是公差为-1的等差数列,则不难通过数列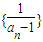 求出数列{an}的通项公式;
求出数列{an}的通项公式;(2)
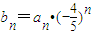 ,说明数列{bn}的奇数项为负数,偶数项为正数.通过作差:|bn+1|-|bn|,化简得|bn+1|-|bn|=
,说明数列{bn}的奇数项为负数,偶数项为正数.通过作差:|bn+1|-|bn|,化简得|bn+1|-|bn|=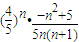 ,讨论得当n=3时,|b3|是数列{|bn|}的最大项,但是b3<0,说明b3是{bn}最小的项,而在正数项中,绝对第二大的项可能是b2或b4,通过作差比较可得b2是数列{bn}的最大项.在此基础之上不难用定义:对于任意的正整数m、n,都有|bn-bm|<ω,则称该数列为“ω域收敛数列”,证明数列{bn}是一个“
,讨论得当n=3时,|b3|是数列{|bn|}的最大项,但是b3<0,说明b3是{bn}最小的项,而在正数项中,绝对第二大的项可能是b2或b4,通过作差比较可得b2是数列{bn}的最大项.在此基础之上不难用定义:对于任意的正整数m、n,都有|bn-bm|<ω,则称该数列为“ω域收敛数列”,证明数列{bn}是一个“ 域收敛数列”了.
域收敛数列”了.解答:证:(1)因为
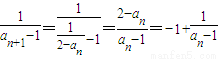 ,
,所以
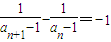 ,n∈N*;
,n∈N*;故
 是等差数列.
是等差数列.由此可得,
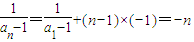 ,
,所以
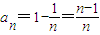 ,n∈N*.
,n∈N*.(2)由条件
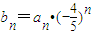 ,
,可知当n=2k,bn>0;当n=2k-1时,bn≤0,k∈N*.
令
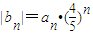 ,则
,则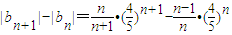 =
=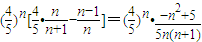 .
.∴当-n2+5>0⇒n≤2时,|bn+1|>|bn|;
同理可得,当-n2+5<0⇒n≥3时,|bn+1|<|bn|;
即数列{|bn|}在n=1,2,3时递增;n≥4时,递减;
即|b3|是数列{|bn|}的最大项.
然而,因为{bn}的奇数项均为-|bn|,故
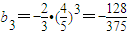 为数列{bn}的最小项;
为数列{bn}的最小项;而
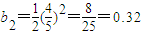 ,
,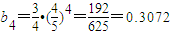 ,
,所以b2>b4,故b2是数列{bn}的最大项.
∴对任意的正整数m、n,
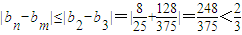 ,
,∴数列
 ,n∈N*是一个“
,n∈N*是一个“ 域收敛数列”.
域收敛数列”.点评:本题是一道由一个数列为基础,同时考查了函数不等式的相关知识,属于难题.着重考查数列的性质和应用,解题时要注意认真审题,仔细计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|