摘要:22. 在平面直角坐标系中.为坐标原点.已知两点..若点满足().点的轨迹与抛物线:交于 .两点. (Ⅰ)求证:⊥, (Ⅱ)在轴上是否存在一点.使得过点直线交抛物线于D.E两点.并以该弦DE为直径的圆都过原点.若存在.请求出的值及圆心的轨迹方程,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_4465981[举报]
(本小题满分14分)
在平面直角坐标系![]() 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切
相切
于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)试探究圆![]() 上是否存在异于原点的点
上是否存在异于原点的点![]() ,使
,使![]() 到椭圆右焦点F的距离等于
到椭圆右焦点F的距离等于
![]()
![]() 线段
线段![]() 的长.若存在,请求出点
的长.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(本小题满分14分)
在平面直角坐标系![]() 中,已知圆心在第二象限、半径为
中,已知圆心在第二象限、半径为![]() 的圆
的圆![]() 与直线
与直线![]() 相切
相切
于坐标原点![]() .椭圆
.椭圆![]() 与圆
与圆![]() 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)试探究圆![]() 上是否存在异于原点的点
上是否存在异于原点的点![]() ,使
,使![]() 到椭圆右焦点F的距离等于
到椭圆右焦点F的距离等于
![]()
![]() 线段
线段![]() 的长.若存在,请求出点
的长.若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
.(本小题满分14分)
在平面直角坐标系上,设不等式组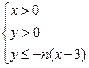 (
(
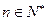 )所表示的平面区域为
)所表示的平面区域为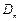 ,记
,记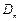 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为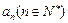 .(Ⅰ)求
.(Ⅰ)求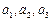 并猜想
并猜想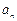 的表达式再用数学归纳法加以证明;(Ⅱ)设数列
的表达式再用数学归纳法加以证明;(Ⅱ)设数列 的前r项和为
的前r项和为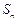 ,数列
,数列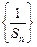 的前r项和
的前r项和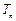 ,是否存在自然数m?使得对一切
,是否存在自然数m?使得对一切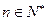 ,
,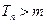 恒成立。若存在,求出m的值,若不存在,请说明理由。
恒成立。若存在,求出m的值,若不存在,请说明理由。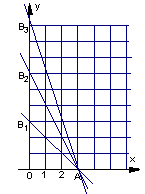
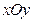 中,已知椭圆
中,已知椭圆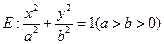 过点
过点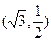 ,且椭圆
,且椭圆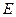 的离心率为
的离心率为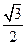
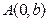 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆 若存在,求出共有几个;若不存在,请说明理由
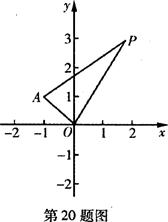
若存在,求出共有几个;若不存在,请说明理由 ,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.