摘要：8．如图.在⊿ABC中.AB⊥AC.AD⊥BC.D是垂足.则.类似有命题:“三棱锥A-BCD(图2)中.AD⊥平面ABC.AO⊥平面BCD.O为垂足.且O在⊿BCD内.则 .上述命题是-----------------------------( ) (A) 真命题 (B) 假命题 (C) 增加AB⊥AC的条件才是真命题 (D) 增加三棱锥A-BCD是正三棱锥的 条件才是真命题
网址：http://m.1010jiajiao.com/timu3_id_4465280[举报]
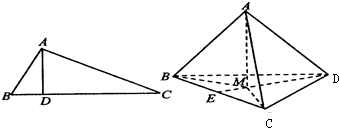如图，在△ABC中，AB⊥AC，若AD⊥BC，则AB2=BD•BC；类似地有命题：在三棱锥A-BCD中，AD⊥面ABC，若A点在BCD内的射影为M，则有| S | 2 △ABC |
查看习题详情和答案>>
如图，在△ABC中，∠B=90°，以AB为直径的⊙O交AC于D，点E为BC的中点，连接DE、AE，AE交⊙O于点F。
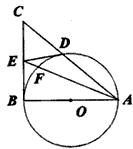
（1）求证：DE是⊙O的切线；
（2）若⊙O的直径为2，求AD·AC的值。
查看习题详情和答案>>
（2）若⊙O的直径为2，求AD·AC的值。
如图1，在△ABC中AB⊥AC、AD⊥BC，D是垂足，则AB2=BD•BC（射影定理）．类似的有命题：在三棱锥A-BCD（图2）中，AD⊥平面ABC，AO⊥平面BCD，O为垂足，且O在△BCD内，则（S△ABC）2=S△BCO•S△BCD（S表示面积．上述命题（ ）
查看习题详情和答案>>
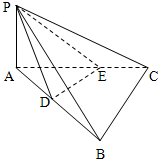如图，在三棱锥P-ABC中，PA⊥平面ABC，AB=BC=CA=2PA，D、E分别是棱AB，AC上的动点，且AD=CE，连接DE，当三棱锥P-ADE体积最大时，平面PDE和平面PBC所成二面角的余弦值为（ ）
如图，在三棱锥P-ABC中，PA⊥AC，PA⊥AB，PA=PB，∠ABC=
，∠BCA=
，点D、E分别在棱PB，PC上，且DE∥BC，