题目内容
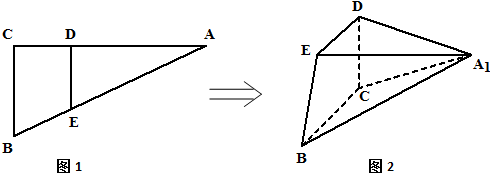
如图1,在△ABC中AB⊥AC、AD⊥BC,D是垂足,则AB2=BD•BC(射影定理).类似的有命题:在三棱锥A-BCD(图2)中,AD⊥平面ABC,AO⊥平面BCD,O为垂足,且O在△BCD内,则(S△ABC)2=S△BCO•S△BCD(S表示面积.上述命题( )


分析:通过连接DO,据BC⊥AO,BC⊥AD得到BC⊥面ADE,得到BC⊥ED得到满足平面条件的三角形AED,利用平面三角形的性质得证.
解答:解:命题是一个真命题.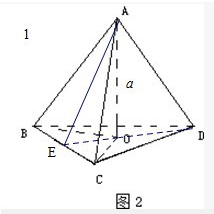
在图(2)中,连接DO,并延长交BC于E,连接AE,则有OE⊥BC.
因为AO⊥面ABC,所以AO⊥AE.
又AO⊥DE,所以AE2=EO•ED.
于是S△ABC2=(
BC•AE)2(
BC•EO)•(
BC•ED)=S△BCO•S△BCD.
故有S△ABC2=S△BCO•S△BCD.
故选A.

在图(2)中,连接DO,并延长交BC于E,连接AE,则有OE⊥BC.
因为AO⊥面ABC,所以AO⊥AE.
又AO⊥DE,所以AE2=EO•ED.
于是S△ABC2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故有S△ABC2=S△BCO•S△BCD.
故选A.
点评:本题考查类比推理及利用平面的性质证明空间的结论.考查空间想象能力,难度较大.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目