��Ŀ����
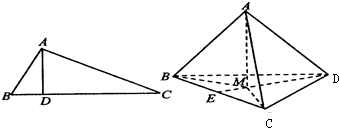 ��ͼ���ڡ�ABC�У�AB��AC����AD��BC����AB2=BD•BC�����Ƶ������⣺������A-BCD�У�AD����ABC����A����BCD�ڵ���ӰΪM������
��ͼ���ڡ�ABC�У�AB��AC����AD��BC����AB2=BD•BC�����Ƶ������⣺������A-BCD�У�AD����ABC����A����BCD�ڵ���ӰΪM������| S | 2 ��ABC |
����������AE��֤��AM��DE��AD��AE������Ӱ�����ɵ�AE2=EM•ED���ٽ�������ε������ʽ�ɵý��ۣ�
����⣺����AE����
��ΪAD����ABC��AE?��ABC��
����AD��AE��
��AM��DE��
��������Ӱ�����ɵ�AE2=EM•ED��
����S��ABC2=(
BC•AM)2=
BC•EM•
BC•MD=S��BCM•S��BCD��
����S��ABC2=S��BCM•S��BCD��
����������һ�������⣮
��ѡA��
��ΪAD����ABC��AE?��ABC��
����AD��AE��
��AM��DE��
��������Ӱ�����ɵ�AE2=EM•ED��
����S��ABC2=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
����S��ABC2=S��BCM•S��BCD��
����������һ�������⣮
��ѡA��
���������⿼���������������ƽ�������֤���ռ�Ľ��ۣ�����ռ�����������֤��AE2=EO•ED�ǹؼ���

��ϰ��ϵ�д�
 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
�����Ŀ
 ��ͼ���ڡ�ABC�У�D�DZ�AC�ϵĵ㣬��AB=AD��2AB=
��ͼ���ڡ�ABC�У�D�DZ�AC�ϵĵ㣬��AB=AD��2AB=| 3 |
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
 ��ͼ���ڡ�ABC�У���֪��ABC=90�㣬AB��һ��E����BEΪֱ���ġ�Oǡ��AC�����ڵ�D����AE=2cm��
��ͼ���ڡ�ABC�У���֪��ABC=90�㣬AB��һ��E����BEΪֱ���ġ�Oǡ��AC�����ڵ�D����AE=2cm�� ��ͼ���ڡ�ABC�У���
��ͼ���ڡ�ABC�У��� ��ͼ���ڡ�ABC�У���B=45�㣬D��BC���ϵ�һ�㣬AD=5��AC=7��DC=3��
��ͼ���ڡ�ABC�У���B=45�㣬D��BC���ϵ�һ�㣬AD=5��AC=7��DC=3�� ��ͼ���ڡ�ABC�У���֪
��ͼ���ڡ�ABC�У���֪