摘要：在平面向量中.如果.不共线.并且=(1-t) +t,则A.B.P共线.拓展到空间.对空间任意一点O和不共线的三点A.B.C.如果四点共面.则有 .
网址：http://m.1010jiajiao.com/timu3_id_4464724[举报]
在平面向量中，下列说法正确的是( )
A.如果两个向量的长度相等，那么这两个向量相等
B.如果两个向量平行，那么这两个向量的方向相同
C.如果两个向量平行并且它们的模相等，那么这两个向量相等
D.同向且等长的有向线段表示同一向量
查看习题详情和答案>>
在平面直角坐标系xOy中，已知圆x2+y2-12x+32=0的圆心为Q，过点P（0，2）且斜率为k的直线l与圆Q相交于不同的两点A，B．
（Ⅰ）求圆Q的面积；
（Ⅱ）求k的取值范围；
（Ⅲ）是否存在常数k，使得向量
+
与
共线？如果存在，求k的值；如果不存在，请说明理由．
查看习题详情和答案>>
（Ⅰ）求圆Q的面积；
（Ⅱ）求k的取值范围；
（Ⅲ）是否存在常数k，使得向量
| OA |
| OB |
| PQ |
平面向量
=(
，-1)，
=(
，
)，若存在不同时为o的实数k和x，使
=
+(x2-3)
，
=-k
+x
，
⊥
．
（Ⅰ）试求函数关系式k=f（x）．
（Ⅱ）对（Ⅰ）中的f（x），设h（x）=4f（x）-ax2在[1，+∞）上是单调函数．
①求实数a的取值范围；
②当a=-1时，如果存在x0≥1，h（x0）≥1，且h（h（x0））=x0，求证：h（x0）=x0．
查看习题详情和答案>>
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| m |
| a |
| b |
| n |
| a |
| b |
| m |
| n |
（Ⅰ）试求函数关系式k=f（x）．
（Ⅱ）对（Ⅰ）中的f（x），设h（x）=4f（x）-ax2在[1，+∞）上是单调函数．
①求实数a的取值范围；
②当a=-1时，如果存在x0≥1，h（x0）≥1，且h（h（x0））=x0，求证：h（x0）=x0．
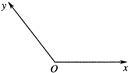如图，在平面斜坐标系xOy中，∠xOy=135°．斜坐标定义：如果