摘要：在椭圆=1上有一点P.F1.F2是椭圆的左右焦点.△F1PF2为直角三角形.则这样的点P有( ) A.2个 B.4个 C.6个 D.8个
网址：http://m.1010jiajiao.com/timu3_id_4464006[举报]
设F1、F2分别为椭圆C：
+
=1的左、右两个焦点．
（1）若椭圆C上的点A（1，
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标．
（2）已知圆心在原点的圆具有性质：若M、N是圆上关于原点对称的两点，点P是圆上的任意一点，当直线PM、PN的斜率都存在，并记作KPM、KPN那么KPMKPN=-1．试对椭圆
+
=1写出类似的性质，并加以证明．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
（1）若椭圆C上的点A（1，
| 3 |
| 2 |
（2）已知圆心在原点的圆具有性质：若M、N是圆上关于原点对称的两点，点P是圆上的任意一点，当直线PM、PN的斜率都存在，并记作KPM、KPN那么KPMKPN=-1．试对椭圆
| x2 |
| a2 |
| y2 |
| b2 |
设F1、F2分别为椭圆C：
+
=1（a＞b＞0）的左、右两个焦点．
（1）若椭圆C上的点A（1，
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程；
（3）已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN时，那么kPM与kPN之积是与点P位置无关的定值．试对双曲线
-
=1写出具有类似特性的性质，并加以证明．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
（1）若椭圆C上的点A（1，
| 3 |
| 2 |
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程；
（3）已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN时，那么kPM与kPN之积是与点P位置无关的定值．试对双曲线
| x2 |
| a2 |
| y2 |
| b2 |
（14分）设F1、F2分别为椭圆C：
=1（a＞b＞0）的左、右两个焦点.
（1）若椭圆C上的点A（1，
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标；
（2）设点K是（1）中所得椭圆上的动点，求线段F1K的中点的轨迹方程；
（3）已知椭圆具有性质：若M、N是椭圆C上关于原点对称的两个点，点P是椭圆上任意一点，当直线PM、PN的斜率都存在，并记为kPM、kPN时，那么kPM与kPN之积是与点P位置无关的定值.试对双曲线
写出具有类似特性的性质，并加以证明．
查看习题详情和答案>>
=1（a＞b＞0）的左、右两个焦点.
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标；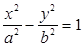
写出具有类似特性的性质，并加以证明．
+
=1（a＞b＞0）的左、右两个焦点．
）到F1、F2两点的距离之和等于4，写出椭圆C的方程和焦点坐标；
），求|PQ|的最大值；