摘要:(1) (A) (B) (C) (D) (2)已知 (A) (B) (C) (D) (3)设函数若 (A) (B) (C) (D) (4)O是平面上一定点.A.B.C是平面上不共线的三个点.动点P满足 则P的轨迹一定通过的 内心 垂心 (5)函数的反函数为 (A) (B) (C) (D) (6)棱长为的正方体中.连结相邻面的中心.以这些线段为棱的八面体的体积为 (A) (B) (C) (D) (7)设曲线处切线的倾斜角的取值范围为则对称轴距离的取值范围为 (A) (B) (C) (D) (8)已知方程的四个根组成一个首项为的等差数列.则 (C) (D) (9)已知双曲线中心在原点且一个焦点为.直线与其交于两点. 中点的横坐标为.则此双曲线的方程是 (A)(B) (C) (D) (10)已知长方形的四个顶点A(0,0).B(2,0).C(2,1)和D(0,1).一质点从AB的中点P0沿与AB夹角为的方向射到BC上的点P1后.依次反射到CD.DA和AB上的点P2.P3和 P4.设P4的坐标为().若.则的取值范围是 (A) (B) (C) (D) (11) (C) (D)6 (12)一个四面体的所有棱长都为.四个顶点在同一球面上.则此球的表面积为 (A) (B) (C) (D) 普通高等学校招生全国统一考试 数 学 第Ⅱ卷
网址:http://m.1010jiajiao.com/timu3_id_4463742[举报]
设函数f(x),g(x)的定义域分别为F、G,且F、G.若对任意的x∈F,都有g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数”.已知函数f(x)=2x(x≤0),若g(x)为f(x)在R上一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是( )
| A、g(x)=2|x| | ||
| B、g(x)=log2|x| | ||
C、g(x)=(
| ||
D、g(x)=log
|
设函数y=f(x)在(a,b)上的导函数为f′(x),f′(x)在(a,b)上的导函数为f″(x),若在a,b)上,f″(x)<0恒成立,则称函数函数f(x)在(a,b)上为“凸函数”.已知当m≤2时,f(x)=
x3-
mx2+x在(-1,2)上是“凸函数”.则f(x)在(-1,2)上( )
| 1 |
| 6 |
| 1 |
| 2 |
| A、既有极大值,也有极小值 |
| B、既有极大值,也有最小值 |
| C、有极大值,没有极小值 |
| D、没有极大值,也没有极小值 |
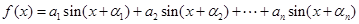 ,其中
,其中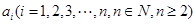 为已知实数,
为已知实数,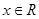 ,则下列各命题中错误的是( )
,则下列各命题中错误的是( ) ,则
,则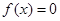 对任意实数恒成立;
对任意实数恒成立;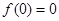 ,则函数
,则函数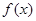 为奇函数;
为奇函数;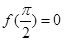 ,则函数
,则函数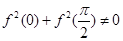 时,若
时,若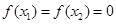 ,则
,则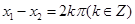
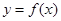 在
在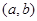 上的导函数为
上的导函数为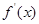 ,
,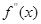 ,若在
,若在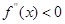 恒成立,则称函数
恒成立,则称函数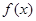 在
在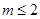 时,
时,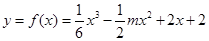 在
在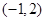 上是“凸函数”,则
上是“凸函数”,则