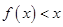题目内容
设函数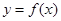 在
在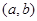 上的导函数为
上的导函数为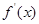 ,
,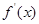 在
在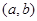 上的导函数为
上的导函数为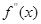 ,若在
,若在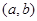 上,
上,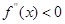 恒成立,则称函数
恒成立,则称函数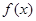 在
在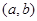 上为“凸函数”.已知当
上为“凸函数”.已知当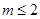 时,
时,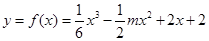 在
在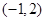 上是“凸函数”,则
上是“凸函数”,则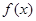 在
在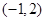 上( )
上( )
A.既没有最大值,也没有最小值 B.既有最大值,也有最小值
C.有最大值,没有最小值 D.没有最大值,有最小值
【答案】
A
【解析】
试题分析: ,因为
,因为 在
在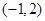 上是“凸函数”,
上是“凸函数”,
所以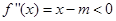 在
在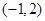 上恒成立,所以
上恒成立,所以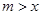 在
在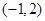 上恒成立,故
上恒成立,故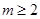 ,
,
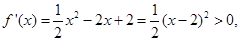 所以
所以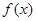 在
在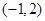 上既没有最大值,也没有最小值.
上既没有最大值,也没有最小值.
考点:1.恒成立问题;2.导数.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 在
在 上的导函数为
上的导函数为 ,
, ,若在
,若在 恒成立,则称函数
恒成立,则称函数 在
在 .
.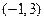 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数 的值;
的值; 时,函数
时,函数 的最大值.
的最大值.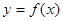 在
在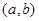 上的导函数为
上的导函数为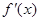 ,
,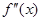 ,若在
,若在 恒成立,则称函数
恒成立,则称函数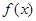 在
在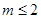 时,
时,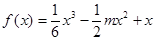 在
在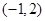 上是“凸函数”.则
上是“凸函数”.则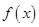 在
在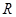 上的导函数为
上的导函数为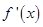 ,且
,且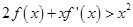 ,下面的不等式在
,下面的不等式在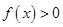 B.
B.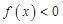 C.
C. 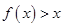 D.
D.