摘要：本小题满分12分 设函数的定义域是R.对于任意实数.恒有.且当 时.． (Ⅰ)求证:.且当时.有, (Ⅱ)判断在R上的单调性, (Ⅲ)设集合.集合.若.求的取值范围． 解:(1).令.则.且由时..所以,--------------------------------------2分 设..．-----4分 (2).则时..----------------------------6分 .在R上单调递减．-------------------------8分 (3).由单调性知.---9分 又.---------------------------------------10分 ...从而．---------12分
网址：http://m.1010jiajiao.com/timu3_id_4463187[举报]
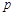：函数f(x)＝x3－ax－1在区间
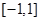上单调递减；命题
：函数
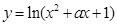的定义域是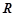
．如果命题
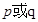为真命题，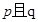
为假命题，求
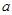的取值范围．(本小题满分12分)
已知函数
，
(1)
若
，
，且
的定义域是[– 1，1]，P（x1，y1），Q（x2，y2）是其图象上任意两点（
），设直线PQ的斜率为k，求证：
；
(2) 若
，且的定义域是
，
．
求证：
．
查看习题详情和答案>>
，
，
，且
的定义域是[– 1，1]，P（x1，y1），Q（x2，y2）是其图象上任意两点（
），设直线PQ的斜率为k，求证：
；
，且
，
．
．