摘要:19. 如图是表示以AB=4.BC=3的矩形ABCD为底面的长方体被一平面斜截所得的几何体.其中四边形EFGH为截面.已知AE=5.BF=8.CG=12. (Ⅰ)作出截面EFGH与底面ABCD的交线l, (Ⅱ)截面四边形EFGH是否为菱形?并证明你的结论, (Ⅲ)求DH的长, (Ⅳ)求截面EFGH与底面ABCD所成锐角的余弦值.
网址:http://m.1010jiajiao.com/timu3_id_4462944[举报]
 (2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
(2013•宿迁一模)【选做题】本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.选修4-1:几何证明选讲
如图,已知AB,CD是圆O的两条弦,且AB是线段CD的 垂直平分线,若AB=6,CD=2
| 5 |
B.选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M=
|
C.选修4-4:坐标系与参数方程(本小题满分10分)
在平面直角坐标系xOy中,已知曲线C的参数方程是
|
D.选修4-5:不等式选讲(本小题满分10分)
已知关于x的不等式|ax-1|+|ax-a|≥1的解集为R,求正实数a的取值范围.
(本小题满分16分)
高 已知数列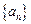 的前
的前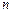 项和为
项和为 ,且满足
,且满足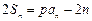 ,
,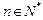 ,其中常数
,其中常数 .
.
(1)证明:数列 为等比数列;
为等比数列;
(2)若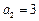 ,求数列
,求数列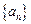 的通项公式;
的通项公式;
(3)对于(2)中数列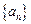 ,若数列
,若数列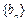 满足
满足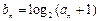 (
(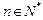 ),在
),在 与
与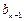 之间插入
之间插入 (
(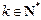 )个2,得到一个新的数列
)个2,得到一个新的数列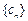 ,试问:是否存在正整数m,使得数列
,试问:是否存在正整数m,使得数列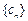 的前m项的和
的前m项的和 ?如果存在,求出m的值;如果不存在,说明理由.
?如果存在,求出m的值;如果不存在,说明理由.
(本小题满分12分)
已知等差数列{an}中a2=8,S10=185.
(1)求数列{an}的通项公式an;
(2)若从数列{an}中依次取出第2,4,8,…,2n,…项,按原来的顺 序排成一个新数列{bn},试求{bn}的前n项和An.
序排成一个新数列{bn},试求{bn}的前n项和An.
 ;(2)
;(2) .试问这两个函数模
.试问这两个函数模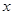 年的年平均费用
年的年平均费用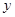 (万元);
(万元);