摘要: 设函数与数列满足关系: ①,其中是方程的实数根, ②, ③的导数. (Ⅰ) 证明:, (Ⅱ) 判断与的大小,并证明你的结论. 第4页
网址:http://m.1010jiajiao.com/timu3_id_4462634[举报]
(本小题满分12分)设函数![]() 的定义域为
的定义域为![]() ,当
,当![]() 时,
时,![]() ,且对于任意的实数
,且对于任意的实数![]() 、
、![]() ,都有
,都有![]() .(1)求
.(1)求![]() ;(2)试判断函数
;(2)试判断函数![]() 在
在![]() 上是否存在最小值,若存在,求该最小值;若不存在,说明理由;(3)设数列
上是否存在最小值,若存在,求该最小值;若不存在,说明理由;(3)设数列![]() 各项都是正数,且满足
各项都是正数,且满足![]() ,
,![]() (
(![]() ),又设
),又设![]() ,
,![]() ,
,
![]() , 当
, 当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
(本小题满分12分)
(理)已知函数![]() 取得极小值
取得极小值![]() .
.
(Ⅰ)求a,b的值;
(Ⅱ)设直线![]() . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:
(1)直线l与曲线S相切且至少有两个切点;
(2)对任意x∈R都有![]() . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
试证明:直线![]() 是曲线
是曲线![]() 的“上夹线”.
的“上夹线”.
(本小题满分12分)
已知定义在R上的函数 满足条件:
满足条件: 对非零实数
对非零实数 ,
,
都有
(1) 求函数 的解析式;
的解析式;
(2) 设函数 直线
直线 分别与函数
分别与函数 的反函数
的反函数 交于A,B两点(其中
交于A,B两点(其中 ),设
),设 为数列
为数列 的前
的前 项和.求证:当
项和.求证:当 时,总有
时,总有 成立.
成立.
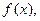 满足条件:
满足条件: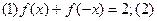 对非零实数
对非零实数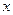 ,
,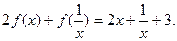
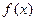 的解析式;
的解析式;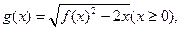 直线
直线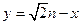 分别与函数
分别与函数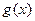 的反函数
的反函数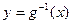 交于A,B两点(其中
交于A,B两点(其中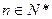 ),设
),设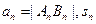 为数列
为数列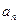 的前
的前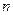 项和.求证:当
项和.求证:当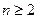 时,总有
时,总有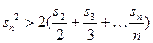 成立.
成立. f(-1-log3
f(-1-log3 =1
(n∈N*);
=1
(n∈N*);