摘要:函数的图象与其反函数图像的交点坐标为 .
网址:http://m.1010jiajiao.com/timu3_id_4462541[举报]
在研究“原函数图象与其反函数的图象的交点是否在直线y=x上”这个课题时,我们可以分三步进行研究:
①首先选取如下函数:y=2x+1,y=
,y=-
;
②求出以上函数的图象与其反函数的图象的交点坐标:y=2x+1与其反函数y=
的图象的交点坐标为(-1,-1);y=
与其反函数y=
的图象的交点坐标为(0,0)、(1,1);y=-
与其反函数y=x2-1(x≤0)的图象的交点坐标为(
,
),(-1,0),(0,-1);
③观察分析上述结果,可得出研究结论为 .
查看习题详情和答案>>
①首先选取如下函数:y=2x+1,y=
| 2x |
| x+1 |
| x+1 |
②求出以上函数的图象与其反函数的图象的交点坐标:y=2x+1与其反函数y=
| x-1 |
| 2 |
| 2x |
| x+1 |
| x |
| 2-x |
| x+1 |
1-
| ||
| 2 |
1-
| ||
| 2 |
③观察分析上述结果,可得出研究结论为
16、给出下列4个命题:
①若一个函数的图象与其反函数的图象有交点,则交点一定在直线y=x上;
②函数y=f(1-x)的图象与函数y=f(1+x)的图象关于直线x=1对称;
③若奇函数y=f(x)的图象关于直线x=a对称,则y=f(x)的周期为2a;
④已知集合A={1,2,3},B={4,5},则以A为定义域,以B为值域的函数有8个.
在上述四个命题中,所有不正确命题的序号是
查看习题详情和答案>>
①若一个函数的图象与其反函数的图象有交点,则交点一定在直线y=x上;
②函数y=f(1-x)的图象与函数y=f(1+x)的图象关于直线x=1对称;
③若奇函数y=f(x)的图象关于直线x=a对称,则y=f(x)的周期为2a;
④已知集合A={1,2,3},B={4,5},则以A为定义域,以B为值域的函数有8个.
在上述四个命题中,所有不正确命题的序号是
①②③④
. 上;
上;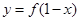 的图象与函数
的图象与函数 的图象关于直线x=1对称;
的图象关于直线x=1对称;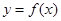 的图象关于直线x=a对称,则
的图象关于直线x=a对称,则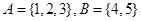 ,则以A为定义域,以B为值域的函数有8个。
,则以A为定义域,以B为值域的函数有8个。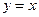 上;
上; 的图象与函数
的图象与函数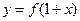 的图象关于直线x=1对称;
的图象关于直线x=1对称; 的图象关于直线x=a对称,则
的图象关于直线x=a对称,则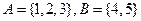 ,则以A为定义域,以B为值域的函数有8个。
,则以A为定义域,以B为值域的函数有8个。