题目内容
在研究“原函数图象与其反函数的图象的交点是否在直线y=x上”这个课题时,我们可以分三步进行研究:
①首先选取如下函数:y=2x+1,y=
,y=-
;
②求出以上函数的图象与其反函数的图象的交点坐标:y=2x+1与其反函数y=
的图象的交点坐标为(-1,-1);y=
与其反函数y=
的图象的交点坐标为(0,0)、(1,1);y=-
与其反函数y=x2-1(x≤0)的图象的交点坐标为(
,
),(-1,0),(0,-1);
③观察分析上述结果,可得出研究结论为 .
①首先选取如下函数:y=2x+1,y=
| 2x |
| x+1 |
| x+1 |
②求出以上函数的图象与其反函数的图象的交点坐标:y=2x+1与其反函数y=
| x-1 |
| 2 |
| 2x |
| x+1 |
| x |
| 2-x |
| x+1 |
1-
| ||
| 2 |
1-
| ||
| 2 |
③观察分析上述结果,可得出研究结论为
分析:从研究的内容:“y=-
与其反函数y=x2-1(x≤0)的图象的交点坐标为(
,
),(-1,0),(0,-1)”即可看出:原函数图象与其反函数的图象的交点不一定在直线y=x上.
| x+1 |
1-
| ||
| 2 |
1-
| ||
| 2 |
解答:解:通过研究“原函数图象与其反函数的图象的交点是否在直线y=x上”这个课题,从中:
y=-
与其反函数y=x2-1(x≤0)的图象的交点坐标为(
,
),(-1,0),(0,-1);
得到:原函数图象与其反函数的图象的交点不一定在直线y=x上,
故答案为:原函数图象与其反函数的图象的交点不一定在直线y=x上
y=-
| x+1 |
1-
| ||
| 2 |
1-
| ||
| 2 |
得到:原函数图象与其反函数的图象的交点不一定在直线y=x上,
故答案为:原函数图象与其反函数的图象的交点不一定在直线y=x上
点评:本小题主要考查反函数,互为反函数图象的交点等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
相关题目
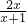 ,y=-
,y=- ;
; 的图象的交点坐标为(-1,-1);y=
的图象的交点坐标为(-1,-1);y=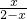 的图象的交点坐标为(0,0)、(1,1);y=-
的图象的交点坐标为(0,0)、(1,1);y=- ,
,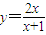 ,
,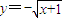
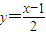 的交点坐标为(-1,-1)
的交点坐标为(-1,-1)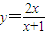 与其反函数
与其反函数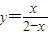 的交点坐标为(0,0),(1,1)
的交点坐标为(0,0),(1,1)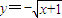 与其反函数y=x2-1,(x≤0)的交点坐标为(
与其反函数y=x2-1,(x≤0)的交点坐标为(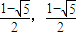 ),(-1,0),(0,-1)
),(-1,0),(0,-1)