题目内容
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为 、
、 、
、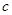 ,且满足
,且满足 .
.
(1)求角B的大小;
|
 ,求
,求 的最小值.
的最小值.
(1) (2) 当
(2) 当 时,
时,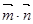 取得最小值0.
取得最小值0.
解析试题分析:解:(1)由正弦定理 ,有
,有 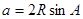 ,
, 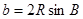 ,
,
代入(2a-c)cosB=bcosC,得(2sinA-sinC)cosB="sinBcosC."
即2sinAcosB=sinBcosC+sinCcosB=sin(B+C)
∵A+B+C=π,∴2sinAcosB="sinA."
∵0<A<π,∴sinA≠0.
∴cosB= .
.
∵0<B<π,∴B= .
.
(2) =-sinA+1
=-sinA+1
由B= 得A∈(0,
得A∈(0, )
)
所以,当 时,
时,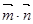 取得最小值0.
取得最小值0.
考点:解三角形
点评:解决的关键是根据已知的边角关系化简变形,结合正弦定理和来得到结论,同时结合向量的数量积来求解最值,属于基础题。

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 ,且c =
,且c = ,C =
,C =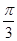 ,求a,b的值
,求a,b的值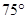 的方向上,距离为
的方向上,距离为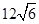 海里,在A处看灯塔C在货轮的北偏西
海里,在A处看灯塔C在货轮的北偏西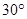 的方向上,距离为
的方向上,距离为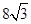 海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东
海里,货轮由A处向正北航行到D处时,再看灯塔B在南偏东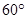 方向上,求:
方向上,求: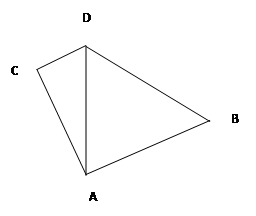
 顶点的分别为
顶点的分别为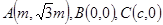 ,其中
,其中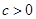 .
.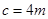 ,求
,求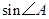 的值;
的值;
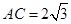 ,求
,求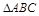 中,
中,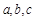 分别是角
分别是角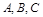 的对边,
的对边, ,
, .
. 的值;
的值; ,求边
,求边 的长.
的长.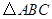 中,内角
中,内角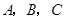 对边的边长分别是
对边的边长分别是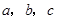 ,已知
,已知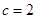 ,
, .
.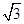 ,求
,求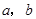 ;
;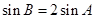 ,求
,求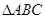 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是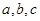 ,
,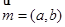 ,
,  ,
, 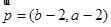
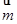 ∥
∥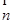 ,求证:
,求证: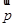 ,边长
,边长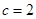 ,
,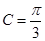 ,求
,求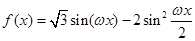 (
(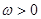 )的最小正周期为
)的最小正周期为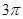 ,
,  时,求函数
时,求函数 的最小值;
的最小值;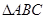 中,若
中,若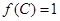 ,且
,且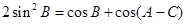 ,求
,求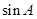 的值。
的值。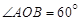 ,
,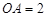 ,
,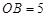 ,在线段
,在线段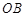 上任取一点
上任取一点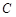 ,
,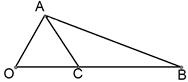
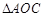 为钝角三角形的概率;
为钝角三角形的概率;