摘要：19]将正方形ABCD折叠.使顶点A与CD边上的点M重合.折痕交AD于E.交BC于F.边AB折叠后与BC边交于点G. (1)如果M为CD边的中点.求证:DE∶DM∶EM=3∶4∶5, (2)如果M为CD边上的任意一点.设AB=2a.问△CMG的周长是否与点M的位置有关?若有关.请把△CMG的周长用含DM的长x的代数式表示,若无关.请说明理由. 答案:(1)先求出DE=..后证之. (2)注意到△DEM∽△CMG.求出△CMG的周长等于4a.从而它与点M在CD边上的位置无关.
网址：http://m.1010jiajiao.com/timu3_id_446200[举报]
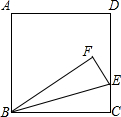将正方形ABCD沿着BE翻折，使C点落在F点处，设∠CBE=x°，∠ABF=y°．若∠ABF=2∠EBF，则列出的关于x、y的方程组正确的是（ ）A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图，将正方形ABCD的一角折叠，折痕为AE，∠BAD比∠BAE大48°．设∠BAE和∠BAD的度数分别为x，y，那么x，y所适合的一个方程组是（ ）A、
| |||||
B、
| |||||
C、
| |||||
D、
|
如图，已知正方形ABCD边长为10cm，点M从C到D以1cm/s的速度运动．将正方形ABCD折叠，使顶点A与点M重合，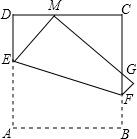
折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G．设点M的运动时间为t（0＜t＜10），单位：s．
（1）求证：△DEM∽△CMG；
（2）当t=5s时，求△DEM的周长；
（3）当5＜t＜10时，求△CMG的周长． 查看习题详情和答案>>
折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G．设点M的运动时间为t（0＜t＜10），单位：s．（1）求证：△DEM∽△CMG；
（2）当t=5s时，求△DEM的周长；
（3）当5＜t＜10时，求△CMG的周长． 查看习题详情和答案>>
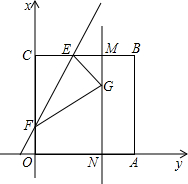（3，0），MN平行于y轴，E是BC的中点，现将纸片折叠，使点C落在MN上，折痕为直线EF，
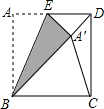（2012•台州）如图，将正方形ABCD沿BE对折，使点A落在对角线BD上的A′处，连接A′C，则∠BA′C=