摘要：已知奇函数y=f∪.值域为R.当且仅当x>1时f有下列命题: ①f=0有无穷多的实数解 ③f(x)存在最小值但无最大值 ④f(x)的图象关于原点对称且是周期函数 其中正确命题是----------- A.①② B.②③ C.①④ D.③④
网址：http://m.1010jiajiao.com/timu3_id_4461698[举报]
已知奇函数f（x）=cos（ωx+φ）（ω＞0，且-π≤φ≤0）的定义域为R，其图象C关于直线x=
对称，又f（x）在区间[0，
]上是单调函数．
（1）求函数f（x）的表达式；
（2）将图象C向右平移
个单位后，得到函数y=g（x）的图象．
①化简，并求值：
+4f（10°）；
②若关于x的方程f（x）=g（x）+m在区间[0，
]上有唯一实根，求实数m的取值范围．
查看习题详情和答案>>
| π |
| 4 |
| π |
| 6 |
（1）求函数f（x）的表达式；
（2）将图象C向右平移
| π |
| 4 |
①化简，并求值：
| 1+f(20°)+g(20°) |
| 1+f(20°)-g(20°) |
②若关于x的方程f（x）=g（x）+m在区间[0，
| π |
| 6 |
已知奇函数f（x）=cos（ωx+φ）（ω＞0，且-π≤φ≤0）的定义域为R，其图象C关于直线x=
对称，又f（x）在区间[0，
]上是单调函数．
（1）求函数f（x）的表达式；
（2）将图象C向右平移个单位后，得到函数y=g（x）的图象．
①化简，并求值：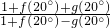
+4f（10°）；
②若关于x的方程f（x）=g（x）+m在区间[0，]上有唯一实根，求实数m的取值范围．
查看习题详情和答案>>
已知奇函数f（x）=cos（ωx+φ）（ω＞0，且-π≤φ≤0）的定义域为R，其图象C关于直线x=
对称，又f（x）在区间[0，
]上是单调函数．
（1）求函数f（x）的表达式；
（2）将图象C向右平移
个单位后，得到函数y=g（x）的图象．
①化简，并求值：
+4f（10°）；
②若关于x的方程f（x）=g（x）+m在区间[0，
]上有唯一实根，求实数m的取值范围．
查看习题详情和答案>>
| π |
| 4 |
| π |
| 6 |
（1）求函数f（x）的表达式；
（2）将图象C向右平移
| π |
| 4 |
①化简，并求值：
| 1+f(20°)+g(20°) |
| 1+f(20°)-g(20°) |
②若关于x的方程f（x）=g（x）+m在区间[0，
| π |
| 6 |