题目内容
3、已知f（x）是定义在R上的奇函数，当x≥0时，值域为[-2，3]，则y=f（x）（x∈R）的值域为（ ）
分析：先根据函数的奇偶性作出函数在y轴左侧的图象，欲求f（x）的值域，分两类讨论：①x＞0；②x＜0．结合图象即可解决问题．
解答：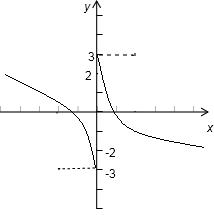
解：∵f（x）是定义在R上的奇函数，
∴作出图象关于原点对称作出其在y轴左侧的图象，如图．
由图可知：f（x）的值域是：
[-2，3]∪[-3，2）=[-3，3]．
故答案为：[-3，3]．
解：∵f（x）是定义在R上的奇函数，∴作出图象关于原点对称作出其在y轴左侧的图象，如图．
由图可知：f（x）的值域是：
[-2，3]∪[-3，2）=[-3，3]．
故答案为：[-3，3]．
点评：本题考查函数的图象，考查同学们对函数基础知识的把握程度以及数形结合的思维能力．易错的地方是不会作出奇函数图象的另一半．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目