摘要： 设., (1)将表示为的函数.并求出的定义域, (2)若关于的方程有且仅有一个实根.求的取值范围. 解:(1) (2)
网址：http://m.1010jiajiao.com/timu3_id_4461581[举报]
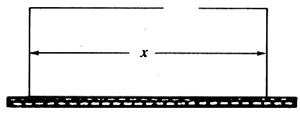
（13分）围建一个面积为
的矩形场地，要求矩形场地的一面利用旧墙(利用的旧墙需维修)，其他三面围墙要新建，在旧墙对面的新墙上要留一个宽度为
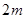的进出口，如图所示。已知旧墙的维修费用为
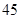元
，新墙的造价为
元。设利用的旧墙长度为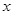
(单位：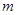
)，修建此矩形场地围墙的总费用为
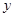(单位：元)。
( I
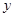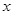)将表示为的函数；
( Ⅱ )试确定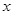，使修建此矩形场地围墙的总费用最小，并求出最小总费用。
查看习题详情和答案>>
某地为促进淡水养殖业的发展，将价格控制在适当范围内，决定对淡水养殖提供政府补贴．设淡水鱼的市场价格为x元/千克，政府补贴为t元/千克，根据市场调查，当8≤x≤14时，淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系：
P＝1 000(x＋t－8)(x≥8，t≥0)，Q＝500
(0≤x≤14)，
当P＝Q时的市场价格称为市场平衡价格．
(1)将市场平衡价格表示为政府补贴的函数，并求出函数的定义域．
(2)为使市场平衡价格不高于每千克10元，政府补贴至少为每千克多少元？
如图所示，
是一个矩形花坛，其中AB= 4米，AD = 3米．现将矩形花坛扩建成一个更大的矩形花园
，要求：B在
上，D在
上，对角线
过C点， 且矩形的面积小于64平方米．
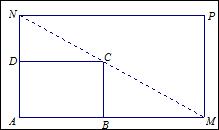
（Ⅰ）设长为
米，矩形的面积为
平方米，试用解析式将表示成的函数，并写出该函数的定义域；
（Ⅱ）当的长度是多少时，矩形的面积最小?并求最小面积．
是一个矩形花坛，其中AB=4米，AD=3米．现将矩形花坛
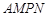，要求：B在
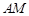上，D在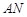
上，对角线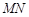
过C点，且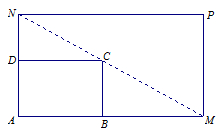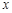矩形
米，矩形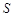
平方米，试用解析式将
是一个矩形花坛，其中AB= 4米，AD = 3米．现将矩形花坛
，要求：B在
上，D在
上，对角线
过C点， 且矩形
米，矩形
平方米，试用解析式将