题目内容
如图所示, 是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛
是一个矩形花坛,其中AB= 4米,AD = 3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园 ,要求:B在
,要求:B在 上,D在
上,D在 上,对角线
上,对角线 过C点, 且矩形
过C点, 且矩形 的面积小于64平方米.
的面积小于64平方米.

(Ⅰ)设 长为
长为 米,矩形
米,矩形 的面积为
的面积为 平方米,试用解析式将
平方米,试用解析式将 表示成
表示成 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当 的长度是多少时,矩形
的长度是多少时,矩形 的面积最小?并求最小面积.
的面积最小?并求最小面积.
【答案】
(1)88 (2)307050 元
【解析】
试题分析:(1)要想求出矩形的面积需要求出AM长,由△NDC∽△NAM可以求出AM的长(2)由第一问可以知道s关于x的函数 ,令
,令 就可以将s转化为基本不等式求解.
就可以将s转化为基本不等式求解.
试题解析:(Ⅰ)由△NDC∽△NAM,可得 ,
,
∴ ,即
,即 ,故
,故 ,
,
由 且
且 ,解得
,解得 ,
,
故所求函数的解析式为 ,定义域为
,定义域为 . 6分
. 6分
(Ⅱ)令 ,则由
,则由 ,可得
,可得 ,
,
故 ,
,
当且仅当 ,即
,即 时,即当
时,即当 时,
时, 取最小值48.
取最小值48.
故当 的长为
的长为 时,矩形
时,矩形 的面积最小,最小面积为
的面积最小,最小面积为 平方米.
12分
平方米.
12分
考点:基本不等式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
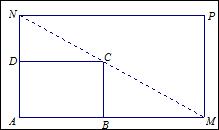
 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,对角线MN过C点,已知|AB|=3米,|AD|=2米,且受地理条件限制,|AN|长不超过8米,设AN=x.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,对角线MN过C点,已知|AB|=3米,|AD|=2米,且受地理条件限制,|AN|长不超过8米,设AN=x.
 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛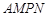 ,要求:B在
,要求:B在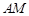 上,D在
上,D在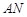 上,对角线
上,对角线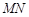 过C点,且矩形
过C点,且矩形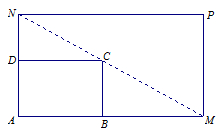
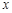 米,矩形
米,矩形 平方米,试用解析式将
平方米,试用解析式将