题目内容
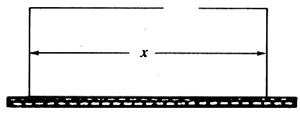
（13分）围建一个面积为
的矩形场地，要求矩形场地的一面利用旧墙(利用的旧墙需维修)，其他三面围墙要新建，在旧墙对面的新墙上要留一个宽度为
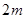的进出口，如图所示。已知旧墙的维修费用为
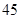元
，新墙的造价为
元。设利用的旧墙长度为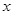
(单位：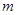
)，修建此矩形场地围墙的总费用为
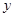(单位：元)。
( I
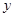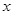)将表示为的函数；
( Ⅱ )试确定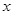，使修建此矩形场地围墙的总费用最小，并求出最小总费用。
【答案】
(Ⅰ)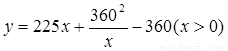
(Ⅱ) 当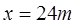
时，修建此矩形场地围墙的总费用最小，最小总费用为10440元。
【解析】略
练习册系列答案
相关题目
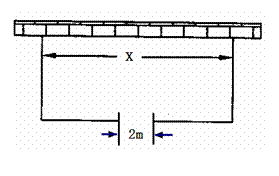如图，围建一个面积为
的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修）,其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为
的一扇门,已知旧墙的维修费用为
元/m,新墙的造价为
元/m,一扇门的造价为
元，设利用的旧墙的长度为
m，总造价为
元.
如图，围建一个面积为
的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修）,其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为
的一扇门,已知旧墙的维修费用为
元/m,新墙的造价为
元/m,一扇门的造价为
元，设利用的旧墙的长度为
m，总造价为
元.
的矩形场地，要求矩形场地ABCD的一面利用旧墙EF（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为
的进出口，如图所示，已知旧墙的维修费用为
,新墙的造价为
,设利用的旧墙的长度为
(单位：
)。
表示为