摘要:如图.AB是⊙O的直径.PA垂直于⊙O所在的平面.C是圆周上不同于A.B的任意一点.求证:平面PAC⊥平面PBC.
网址:http://m.1010jiajiao.com/timu3_id_4461386[举报]
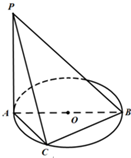 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.(1)证明:△PBC是直角三角形;
(2)若PA=AB=2,且当直线PC与平面ABC所成角正切值为
| 2 |
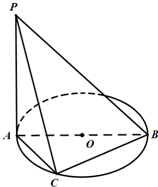 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.(1)证明:面PAC⊥面PBC;
(2)若PA=AB=2,则当直线PC与平面ABC所成角正切值为
| 2 |
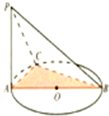 如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,则图中直角三角形有
如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,则图中直角三角形有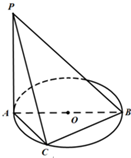
 时,直线AB与平面PBC所成角的正弦值.
时,直线AB与平面PBC所成角的正弦值.