Question

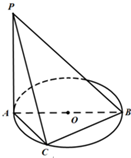如图，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是圆周上不同于A，B的一动点．
（1）证明：△PBC是直角三角形；
（2）若PA=AB=2，且当直线PC与平面ABC所成角正切值为

2

时，直线AB与平面PBC所成角的正弦值．

Answer 1

分析：（1）由C在圆O上，知BC⊥AC，由PA⊥平面ABC，知BC⊥PA，由此能证明△BPC是直角三角形．
（2）过A作AH⊥PC于H，由BC⊥平面PAC，知BC⊥AH，AH⊥平面PBC，所以∠ABH是AC与平面PBC所成角．由此能求出AC与平面PBC所成角正弦值．

解答：（1）证明：∵C在圆O上，∴BC⊥AC，
∵PA⊥平面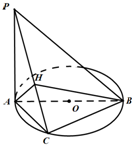ABC，∴BC⊥PA，
∵PC?平面PAC，∴BC⊥平面PAC，
∴BC⊥PC，∴△BPC是直角三角形．
（2）解：如图，过A作AH⊥PC于H，
∵BC⊥平面PAC，∴BC⊥AH，
∴AH⊥平面PBC，则∠ABH就是要求的角．…（8分）
∵PA⊥平面ABC，∴∠PCA是PC与平面ABC所成角，…（9分）
∵tan∠PCA=

PA

AC

=

2

，又PC=2，∴AC=

2

．…（10分）
∴在Rt△PAC中，AH=

PA•AC

PA2+AC2

=

2

3

3

，…（11分）
∴在RtABH中，sin∠ABH=

2 3 3

2

=

3

3

，
故AC与平面PBC所成角正弦值为

3

3

．…（12分）

点评：本题考查直角三角形的证明，考查直线与平面所成角的求法．解题时要认真审题，仔细解答，注意等价转化思想的合理运用．