摘要：如果.不共线.则下列四组向量共线的有-------------------( ) ⑴2.-2,⑵-.-2+2,⑶4-.-,⑷+.2-2 (A)⑵⑶ (B) ⑵⑶⑷ (C) ⑴⑶⑷ (D)⑴⑵⑶⑷
网址：http://m.1010jiajiao.com/timu3_id_4461365[举报]
已知直线m，n，平面α，β，则下列五个命题中正确命题的个数是
①如果a⊥β，m⊥β，则m∥α；
②如果α∥β，m
α，则m∥β；
③如果α∩β＝m，nα，n⊥m，则α⊥β；
④如果α内不共线三点到平面β的距离相等，则α∥β；
⑤如果m∥n，m⊥α，n⊥β，则α∥β．
[ ]
A．1
B．2
C．3
D．4
给出下列命题：
①如果向量
，
，
共面，向量
，
，
也共面，则向量
，
，
，
共面；
②已知直线a的方向向量
与平面α，若
∥平面α，则直线a∥平面α；
③若P、M、A、B共面，则存在唯一实数x、y使
=x
+y
；
④对空间任意点O与不共线的三点A、B、C，若
=x
+y
+z
（其中x+y+z=1），则P、A、B、C四点共面； 在这四个命题中为真命题的序号有 ．
查看习题详情和答案>>
①如果向量
| a |
| b |
| c |
| b |
| c |
| d |
| a |
| b |
| c |
| d |
②已知直线a的方向向量
| a |
| a |
③若P、M、A、B共面，则存在唯一实数x、y使
| MP |
| MA |
| MB |
④对空间任意点O与不共线的三点A、B、C，若
| OP |
| OA |
| OB |
| OC |
定义：对于映射f：A→B，如果A中的不同元素有不同的象，且B中的每一个元素都有原象，则称f：A→B为一一映射．如果存在对应关系φ，使A到B成为一一映射，则称A和B具有相同的势．给出下列命题：
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
，
}，其中
，
是不共线向量，B={
|
与
，
共面的任意向量}，则A和B不可能具有相同的势；
④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为
查看习题详情和答案>>
①A={奇数}，B={偶数}，则A和B 具有相同的势；
②A是直角坐标系平面内所有点形成的集合，B是复数集，则A和B 不具有相同的势；
③若A={
| a |
| b |
| a |
| b |
| c |
| c |
| a |
| b |
④若区间A=（-1，1），B=（-∞，+∞），则A和B具有相同的势．
其中真命题为
①③④
①③④
．
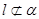，则
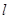不可能与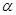
内无数条直线相交。