摘要：D 2.C 3.B 4.A 5.B 6.C 解题指导:
网址：http://m.1010jiajiao.com/timu3_id_446124[举报]
阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：
问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x、y、z元，则需要求x+y+z的值．由题意，知
；
视x为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．
解法1：视x为常数，依题意得
．
解这个关于y、z的二元一次方程组得
．
于是x+y+z=x+0.05+x+1-2x=1.05．
评注：也可以视z为常数，将上述方程组看成是关于x、y的二元一次方程组，解答方法同上，你不妨试试．
分析：视x+y+z为整体，由（1）、（2）恒等变形得5（x+y+z）+4（2x+z）=9.25，4（x+y+z）-（2x+z）=3.20．
解法2：设x+y+z=a，2x+z=b，代入（1）、（2）可以得到如下关于a、b的二元一次方
程组
．
由⑤+4×⑥，得21a+22.05，a=1.05．
评注：运用整体的思想方法指导解题．视x+y+z，2x+z为整体，令a=x+y+z，b=2x+z，代入①、②将原方程组转化为关于a、b的二元一次方程组从而获解．
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表：
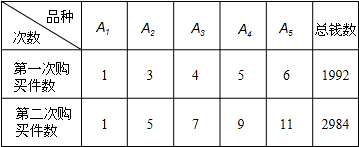
那么，购买每种教学用具各一件共需多少元？ 查看习题详情和答案>>
问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x、y、z元，则需要求x+y+z的值．由题意，知
|
视x为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．
解法1：视x为常数，依题意得
|
解这个关于y、z的二元一次方程组得
|
于是x+y+z=x+0.05+x+1-2x=1.05．
评注：也可以视z为常数，将上述方程组看成是关于x、y的二元一次方程组，解答方法同上，你不妨试试．
分析：视x+y+z为整体，由（1）、（2）恒等变形得5（x+y+z）+4（2x+z）=9.25，4（x+y+z）-（2x+z）=3.20．
解法2：设x+y+z=a，2x+z=b，代入（1）、（2）可以得到如下关于a、b的二元一次方
程组
|
由⑤+4×⑥，得21a+22.05，a=1.05．
评注：运用整体的思想方法指导解题．视x+y+z，2x+z为整体，令a=x+y+z，b=2x+z，代入①、②将原方程组转化为关于a、b的二元一次方程组从而获解．
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表：
那么，购买每种教学用具各一件共需多少元？ 查看习题详情和答案>>
阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：
问题：某人买13个鸡蛋，5个鸭蛋、9个鹅蛋共用去了9.25元；买2个鸡蛋，4个鸭蛋、3个鹅蛋共用去了3.20元．试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元．
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x、y、z元，则需要求x+y+z的值．由题意，知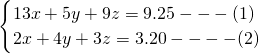
；
视x为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解．
解法1：视x为常数，依题意得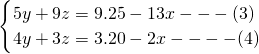
．
解这个关于y、z的二元一次方程组得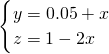
．
于是x+y+z=x+0.05+x+1-2x=1.05．
评注：也可以视z为常数，将上述方程组看成是关于x、y的二元一次方程组，解答方法同上，你不妨试试．
分析：视x+y+z为整体，由（1）、（2）恒等变形得5（x+y+z）+4（2x+z）=9.25，4（x+y+z）-（2x+z）=3.20．
解法2：设x+y+z=a，2x+z=b，代入（1）、（2）可以得到如下关于a、b的二元一次方
程组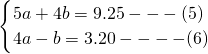
．
由⑤+4×⑥，得21a+22.05，a=1.05．
评注：运用整体的思想方法指导解题．视x+y+z，2x+z为整体，令a=x+y+z，b=2x+z，代入①、②将原方程组转化为关于a、b的二元一次方程组从而获解．
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：
购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表：
那么，购买每种教学用具各一件共需多少元？
查看习题详情和答案>>
阅读下列解题过程，借鉴其中一种方法解答后面给出的试题：
问题：某人买13 个鸡蛋，5 个鸭蛋、9 个鹅蛋共用去了9.25 元；买2 个鸡蛋，4 个鸭蛋、3 个鹅蛋共用去了3.20 元，试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元。
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x 、y 、z 元，则需要求x+y+z 的值，
由题意，知
；
视x为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解。
解法1：视x为常数，依题意得
解这个关于y、z的二元一次方程组得
于是x+y+z=x+0.05+x+1-2x=1.05。
评注：也可以视z为常数，将上述方程组看成是关于x、y的二元一次方程组。
解答方法同上，你不妨试试．分析：视x+y+z为整体，由（1）、（2）恒等变形得
5（x+y+x）+4（2x+z）=9.25，4（x+y+z）-（2x+z）=3.20。
解法2：设x+y+z=a，2x+z=b，代入（1）、（2）可以得到如下关于a、b的二元一次方程组
由⑤+4×⑥，得21a=22.05，a=1.05。
评注：运用整体的思想方法指导解题，视x+y+z，2x+z为整体，
令a=x+y+z，b=2x+z，代人①、②将原方程组转化为关于a、b的二元一次方程组从而获解。
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表：
问题：某人买13 个鸡蛋，5 个鸭蛋、9 个鹅蛋共用去了9.25 元；买2 个鸡蛋，4 个鸭蛋、3 个鹅蛋共用去了3.20 元，试问只买鸡蛋、鸭蛋、鹅蛋各一个共需多少元。
分析：设买鸡蛋，鸭蛋、鹅蛋各一个分别需x 、y 、z 元，则需要求x+y+z 的值，
由题意，知
； 视x为常数，将上述方程组看成是关于y、z的二元一次方程组，化“三元”为“二元”、化“二元”为“一元”从而获解。
解法1：视x为常数，依题意得
解这个关于y、z的二元一次方程组得
于是x+y+z=x+0.05+x+1-2x=1.05。
评注：也可以视z为常数，将上述方程组看成是关于x、y的二元一次方程组。
解答方法同上，你不妨试试．分析：视x+y+z为整体，由（1）、（2）恒等变形得
5（x+y+x）+4（2x+z）=9.25，4（x+y+z）-（2x+z）=3.20。
解法2：设x+y+z=a，2x+z=b，代入（1）、（2）可以得到如下关于a、b的二元一次方程组
由⑤+4×⑥，得21a=22.05，a=1.05。
评注：运用整体的思想方法指导解题，视x+y+z，2x+z为整体，
令a=x+y+z，b=2x+z，代人①、②将原方程组转化为关于a、b的二元一次方程组从而获解。
请你运用以上介绍的任意一种方法解答如下数学竞赛试题：购买五种教学用具A1、A2、A3、A4、A5的件数和用钱总数列成下表：
那么，购买每种教学用具各一件共需多少元?
查看习题详情和答案>>
为落实“健康第一”的指导思想，大力推进素质教育，促进青少年学生健康成长的重要措施．黄冈市2012年初中毕业升学体育考试作为一定改革：考试项目2012年初中毕业生升学体育考试采取现场测试的方法，共三项：①坐位体前屈；②跳绳；③1000米跑（男生）、800米跑（女生）．某校对九年级学生体育测试情况进行调研，从该校360名九年级学生中抽取了部分学生的成绩（成绩分为A、B、C三个层次）进行分析，绘制了频数分布表与频数分布直方图（如图），请根据图表信息解答下列问题：| 分组 | 频数 | 频率 |
| C | 10 | 0.10 |
| B | 0.50 | |
| A | 40 | |
| 合计 | 1.00 |
（2）如果成绩为A等级的同学属于优秀，请你估计该校九年级约有多少人达到优秀水平？
为落实“健康第一”的指导思想，大力推进素质教育，促进青少年学生健康成长的重要措施．黄冈市2012年初中毕业升学体育考试作为一定改革：考试项目2012年初中毕业生升学体育考试采取现场测试的方法，共三项：①坐位体前屈；②跳绳；③1000米跑（男生）、800米跑（女生）．某校对九年级学生体育测试情况进行调研，从该校360名九年级学生中抽取了部分学生的成绩（成绩分为A、B、C三个层次）进行分析，绘制了频数分布表与频数分布直方图（如图），请根据图表信息解答下列问题：
| 分组 | 频数 | 频率 |
| C | 10 | 0.10 |
| B | 0.50 | |
| A | 40 | |
| 合计 | 1.00 |
（2）如果成绩为A等级的同学属于优秀，请你估计该校九年级约有多少人达到优秀水平？ 查看习题详情和答案>>