摘要： 设a.b是两个实数.A＝{(x.y)|x＝n.y＝na+b.n是整数}.B＝{(x.y)|x＝m.y＝3m2+15.m是整数}.C＝{(x.y)|x2+y2≤144}是xoy平面内的集合.讨论是否存在a和b使得①A∩B≠φ.②(a.b)∈C同时成立.
网址：http://m.1010jiajiao.com/timu3_id_4461221[举报]
设a、b是两个实数，集合A＝{(x，y)|y＝ax＋b，x∈Z}，B＝{(x，y)|y＝3x2＋15，x∈Z}，C＝{(x，y)|x2＋y2≤144}，讨论是否存在实数a和b使得A∩B≠
，(a，b)∈C同时成立．
设A、B分别是直线y＝
x和y＝－x上的两个动点，并且|
|＝
，动点P满足
＝
＋
．记动点P的轨迹为C．
(1)求轨迹C的方程；
(2)若点D的坐标为(0，16)，M、N是曲线C上的两个动点，且
＝λ
，求实数λ的取值范围．
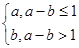设函数f(x)＝(x2－2)?(x－x2)，x∈R，若函数y＝f(x)－c的图象与x轴恰有两个公共点，则实数c的取值范围是_________ .
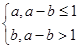设函数f(x)＝(x2－2)?(x－x2)，x∈R，若函数y＝f(x)－c的图象与x轴恰有两个公共点，则实数c的取值范围是_________ .