摘要： 平面直角坐标系是以数轴为基础的.坐标平面内的点的坐标也是利用数轴上点的坐标来定义的.有关直角坐标系的概念比较多.学习时应紧密结合图形.不能死记硬背定义.看到一个概念.脑子里要能马上反映出相关的图形.如对“象限 的理解.关键在于结合直角坐标系.能指出各个象限的位置.进而明确坐标轴上的点不属于任何一个象限的真正含义.
网址：http://m.1010jiajiao.com/timu3_id_446114[举报]
如图，对称轴为直线x=
的抛物线经过点A（6，0）和B（0，4）．
的抛物线经过点A（6，0）和B（0，4）．
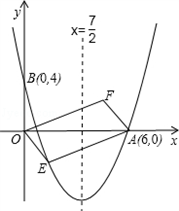
（1）求抛物线解析式及顶点坐标；
（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；
（3）在（2）的基础上试探索：
①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？
②是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．
查看习题详情和答案>>
（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；
（3）在（2）的基础上试探索：
①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？
②是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．
如图，对称轴为直线
的抛物线经过点A（6，0）和B（0，4）。
（1）求抛物线解析式及顶点坐标；
（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量的取值范围；
（3）在（2）基础上试探索：
①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？
②是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由。
的抛物线经过点A（6，0）和B（0，4）。（1）求抛物线解析式及顶点坐标；
（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求平行四边形OEAF的面积S与x之间的函数关系式，并写出自变量的取值范围；
（3）在（2）基础上试探索：
①当平行四边形OEAF的面积为24时，请判断平行四边形OEAF是否为菱形？
②是否存在点E，使平行四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由。
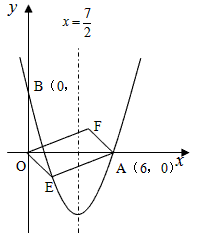
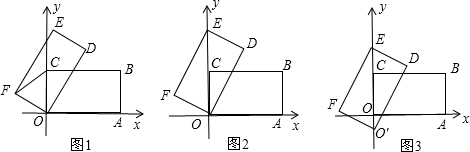
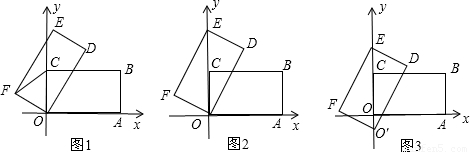
在矩形OABC中，OA=4，AB=2，以点O为坐标原点，OA所在的直线为x轴，建立直角坐标系．将矩形OABC绕点O逆时针旋转至矩形ODEF．
（1）如图1，当∠AOD=60°时，△OCF的形状是 ；
（2）如图2，当点E落在y轴的正半轴上，试求CE的长度和点D的坐标；
（3）如图3，在图2的基础上再沿y轴的负半轴向下平移，平移速度是每秒1个单位长度．
①求经过几秒，直线DE经过点A；
②设两矩形重叠部分的面积为S，运动时间为t，写出重叠部分面积S与时间t之间的函数关系式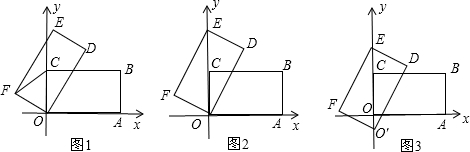
查看习题详情和答案>>
（1）如图1，当∠AOD=60°时，△OCF的形状是
（2）如图2，当点E落在y轴的正半轴上，试求CE的长度和点D的坐标；
（3）如图3，在图2的基础上再沿y轴的负半轴向下平移，平移速度是每秒1个单位长度．
①求经过几秒，直线DE经过点A；
②设两矩形重叠部分的面积为S，运动时间为t，写出重叠部分面积S与时间t之间的函数关系式
查看习题详情和答案>>
