题目内容
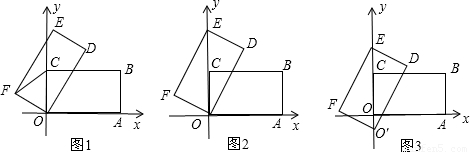
在矩形OABC中,OA=4,AB=2,以点O为坐标原点,OA所在的直线为x轴,建立直角坐标系.将矩形OABC绕点O逆时针旋转至矩形ODEF.(1)如图1,当∠AOD=60°时,△OCF的形状是______;
(2)如图2,当点E落在y轴的正半轴上,试求CE的长度和点D的坐标;
(3)如图3,在图2的基础上再沿y轴的负半轴向下平移,平移速度是每秒1个单位长度.
①求经过几秒,直线DE经过点A;
②设两矩形重叠部分的面积为S,运动时间为t,写出重叠部分面积S与时间t之间的函数关系式
【答案】分析:(1)利用有一个角是60°的三角形是等边三角形即可作出判定;
(2)根据OA=4,OC=2,BC=OA,因而就可求得BC=2CD,则可以求出∠BCD=60°,则旋转角即可求得;作DM⊥CB于点M,FN⊥CB于点N,根据三角函数即可求得:DM,CM的长,从而求得D的坐标,在Rt△CFN中,根据三角函数即可求得CN,FN的长,即得F的坐标;
(3)①HB即为直线EF经过点B时移动的距离.在Rt△C′DH中利用三角函数即可求得DH,从而得到HE,再在△HEB中,利用三角函数求得BH,即可求得时间.
②重合的部分可能是四边形,也可能是三角形,应分两种情况进行讨论.
解答:解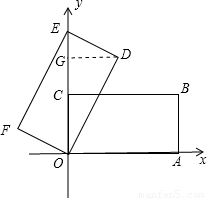 (1)等边三角形…(1分)
(1)等边三角形…(1分)
(2)∵OE= =2
=2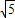 ,OC=2,
,OC=2,
∴CE=2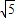 -2…(2分)
-2…(2分)
过点D作DG⊥OE
∵DG•OE=DE•OD
∴DG=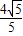
OG=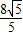
∴D(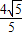 ,
,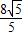 )…(3分)
)…(3分)
(3)①设直线DE所在直线的解析式为y=kx+b,
∵D(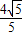 ,
,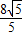 ),E(0,2
),E(0,2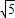 )
)
∴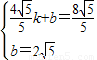
∴DE所在的直线为y=- x+2
x+2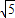
∴平移后DE所在的直线为y=- x+b,把A(4,0)代入得b=2∴平移了2
x+b,把A(4,0)代入得b=2∴平移了2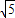 -2 (2
-2 (2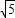 -2)÷1=2
-2)÷1=2 -2(秒)…(5分)
-2(秒)…(5分)
②s=t+1 (0≤t≤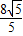 -2)…(6分)
-2)…(6分)
S=- t2+(4
t2+(4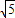 -4)t-20+8
-4)t-20+8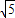 (
(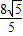 -2<t≤2
-2<t≤2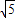 -2)…(7分)
-2)…(7分)
S=4- t2 (2
t2 (2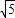 -2<t≤
-2<t≤ )…(8分)
)…(8分)
S=t2-4 t+20 (
t+20 (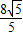 <t≤2
<t≤2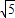 ) …(9分)
) …(9分)
0 (2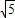 <t) …(10分)
<t) …(10分)
点评:本题是三角函数与图形的旋转相结合的题目,注意旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.得到相等关系是解决本题的关键.
(2)根据OA=4,OC=2,BC=OA,因而就可求得BC=2CD,则可以求出∠BCD=60°,则旋转角即可求得;作DM⊥CB于点M,FN⊥CB于点N,根据三角函数即可求得:DM,CM的长,从而求得D的坐标,在Rt△CFN中,根据三角函数即可求得CN,FN的长,即得F的坐标;
(3)①HB即为直线EF经过点B时移动的距离.在Rt△C′DH中利用三角函数即可求得DH,从而得到HE,再在△HEB中,利用三角函数求得BH,即可求得时间.
②重合的部分可能是四边形,也可能是三角形,应分两种情况进行讨论.
解答:解
 (1)等边三角形…(1分)
(1)等边三角形…(1分)(2)∵OE=
 =2
=2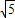 ,OC=2,
,OC=2,∴CE=2
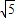 -2…(2分)
-2…(2分)过点D作DG⊥OE
∵DG•OE=DE•OD
∴DG=
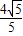
OG=
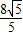
∴D(
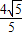 ,
,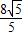 )…(3分)
)…(3分)(3)①设直线DE所在直线的解析式为y=kx+b,
∵D(
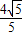 ,
,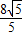 ),E(0,2
),E(0,2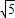 )
)∴
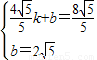
∴DE所在的直线为y=-
 x+2
x+2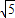
∴平移后DE所在的直线为y=-
 x+b,把A(4,0)代入得b=2∴平移了2
x+b,把A(4,0)代入得b=2∴平移了2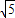 -2 (2
-2 (2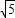 -2)÷1=2
-2)÷1=2 -2(秒)…(5分)
-2(秒)…(5分)②s=t+1 (0≤t≤
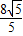 -2)…(6分)
-2)…(6分)S=-
 t2+(4
t2+(4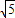 -4)t-20+8
-4)t-20+8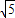 (
(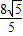 -2<t≤2
-2<t≤2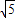 -2)…(7分)
-2)…(7分)S=4-
 t2 (2
t2 (2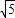 -2<t≤
-2<t≤ )…(8分)
)…(8分)S=t2-4
 t+20 (
t+20 (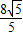 <t≤2
<t≤2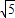 ) …(9分)
) …(9分)0 (2
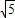 <t) …(10分)
<t) …(10分)点评:本题是三角函数与图形的旋转相结合的题目,注意旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.得到相等关系是解决本题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
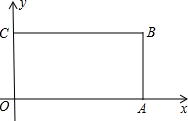 把矩形纸片OABC放人直角坐标系中,使OA、OC分别落在x轴和y轴的正半轴上.
把矩形纸片OABC放人直角坐标系中,使OA、OC分别落在x轴和y轴的正半轴上.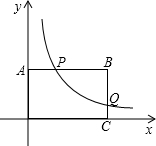 AB的中点,设点P的横坐标为a.
AB的中点,设点P的横坐标为a.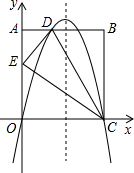 OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
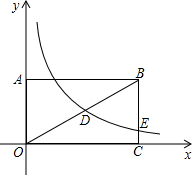 (2013•本溪)如图,在矩形OABC中,AB=2BC,点A在y轴的正半轴上,点C在x轴的正半轴上,连接OB,反比例函数y=
(2013•本溪)如图,在矩形OABC中,AB=2BC,点A在y轴的正半轴上,点C在x轴的正半轴上,连接OB,反比例函数y=