摘要：(13)抛物线的准线方程是 . (14)从1.2.3.4.5中任取两个数.分别作为对数的底数和真数.则可以得到 个不同的对数值. (15)把函数的图象沿x轴向左平移一个单位后.得到图象C.则C关于原点对称的图象的函数解析式为 . (16)长方体一个顶点上三条棱的长分别为a.b.c..一条对角线为AB.长方体的表面上A.B两点间的最短路程为.则a.b.c的大小关系是 .
网址：http://m.1010jiajiao.com/timu3_id_4460791[举报]
设椭圆C1和抛物线C2的焦点均在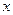
轴上，C1的中心和C2的顶点均为原点，从每条曲线上各取两点，将其坐标记录于下表中：
（1）求曲线C1，C2的标准方程；
（2）设直线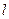
与椭圆C1交于不同两点M、N，且
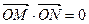。请问是否存在直线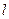过抛物线C2的焦点F？若存在，求出直线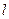的方程；若不存在，请说明理由.
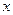轴上，C1的中心和C2的顶点均为原点，从每条曲线上各取两点，将其坐标记录于下表中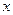： | 3 | -2 | 4 |  |
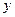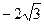 |  | 0 | -4 |  |
（1）求曲线C1，C2的标准方程；
（2）设直线
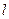与椭圆C1交于不同两点M、N，且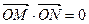。请问是否存在直线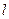过抛物线C2的焦点F？若存在，求出直线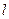的方程；若不存在，请说明理由.已知双曲线C的中心在坐标原点O，两条准线的距离为
，其中一个焦点恰与抛物线x 2 + 10 x 4 y + 21 = 0的焦点重合。
（1）求双曲线C的方程；
（2）若P为C上任意一点，A为双曲线的右顶点，通过P、O的直线与从A所引平行于渐近线的直线分别交于Q、R。试证明：| OP |是| OQ |与| OR |的等比中项。
查看习题详情和答案>>设椭圆C1和抛物线C2的焦点均在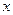
轴上，C1的中心和C2的顶点均为原点，从每条曲线上各取两点，将其坐标记录于下表中：
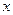| 3 | -2 | 4 |  |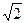
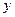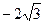 |  | 0 | -4 |  |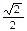
（1）求曲线C1，C2的标准方程；
（2）设直线
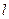与椭圆C1交于不同两点M、N，且
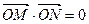。请问是否存在直线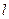过抛物线C2的焦点F？若存在，求出直线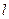的方程；若不存在，请说明理由.
查看习题详情和答案>>