摘要: 已知函数满足 ,且使成立的实数是唯一的. (1) 求函数的解析式.定义域.值域, (2) 如果数列的前项和为.且.试求此数列的前3项.由此猜想数列的通项公式.并予以证明. 解: 有唯一解 由得 ,定义域为. 值域为 (2) , 相减得 即: . 猜想:用数学归类法证明之. (1)当n=1时,分式成立. (2)假设n=k时公式成立.即:. 即n=k+1时分式也成立. 由知恒成立.
网址:http://m.1010jiajiao.com/timu3_id_4460789[举报]
(本小题满分14分) 已知函数![]() 及正整数数列
及正整数数列![]() . 若
. 若![]() ,且当
,且当![]() 时,有
时,有![]() ; 又
; 又![]() ,
,![]() ,且
,且![]() 对任意
对任意![]() 恒成立. 数列
恒成立. 数列![]() 满足:
满足:![]() .
.
(1) 求数列![]() 及
及![]() 的通项公式;
的通项公式;
(2) 求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3) 证明存在![]() ,使得
,使得![]() 对任意
对任意![]() 均成立.
均成立.
(本小题满分14分)
已知函数![]() ,在定义域内有且只有一个零点,存在
,在定义域内有且只有一个零点,存在![]() , 使得不等式
, 使得不等式![]() 成立. 若
成立. 若![]() ,
,![]() 是数列
是数列![]() 的前
的前![]() 项和.
项和.
(I)求数列![]() 的通项公式;
的通项公式;
(II)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的正整数
的正整数![]() 的个数称为这个数列
的个数称为这个数列![]() 的变号数,令
的变号数,令![]() (n为正整数),求数列
(n为正整数),求数列![]() 的变号数;
的变号数;
(Ⅲ)设![]() (
(![]() 且
且![]() ),使不等式
),使不等式
![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
(本小题满分14分) 已知函数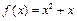 及正整数数列
及正整数数列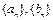 . 若
. 若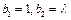 ,且当
,且当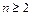 时,有
时,有 ; 又
; 又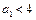 ,
,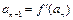 ,且
,且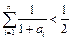 对任意
对任意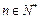 恒成立. 数列
恒成立. 数列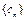 满足:
满足: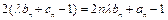 .
.
(1) 求数列 及
及 的通项公式;
的通项公式;
(2) 求数列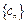 的前
的前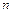 项和
项和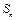 ;
;
(3) 证明存在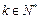 ,使得
,使得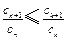 对任意
对任意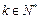 均成立.
均成立.
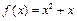 及正整数数列
及正整数数列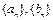 . 若
. 若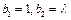 ,且当
,且当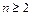 时,有
时,有 ; 又
; 又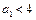 ,
,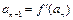 ,且
,且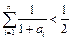 对任意
对任意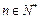 恒成立. 数列
恒成立. 数列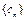 满足:
满足: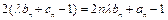 .
.(1) 求数列
 及
及 的通项公式;
的通项公式;(2) 求数列
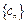 的前
的前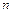 项和
项和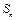 ;
;(3) 证明存在
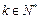 ,使得
,使得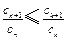 对任意
对任意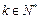 均成立.
均成立. +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为 ,
, .
. 是
是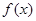 的导函数,且
的导函数,且
 );
); 满足
满足 ,且
,且 ,求数列
,求数列 ,
, ,是否存在自然数
,是否存在自然数 ,使得当
,使得当 时
时
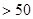 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的 ,
,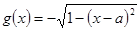 ,
,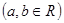
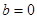 时,若
时,若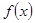 在
在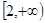 上单调递增,求
上单调递增,求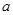 的取值范围;
的取值范围;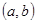 :当
:当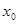 ,使得
,使得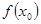 是
是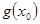 是
是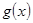 的最小值;
的最小值;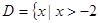 ,且
,且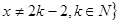 上的函数
上的函数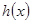 ,使当
,使当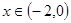 时,
时,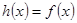 ,当
,当 时,
时,