摘要：21．设函数f(x)=a+与g(x)=x+1.若恒有f(x)≤g(x)成立.试求实数a的取值范围.
网址：http://m.1010jiajiao.com/timu3_id_4460741[举报]
设函数f(x)＝x3＋3ax2＋bx＋c，g(x)＝x2－3x＋2，其中x∈R，a、b为常数，已知曲线y＝f(x)与y＝g(x)在点(2，0)处有相同的切线l．
(Ⅰ)求a、b的值，并写出切线l的方程；
(Ⅱ)若方程f(x)＋g(x)＝mx有三个互不相同的实根0、x1、x2，其中x1＜x2，且对任意的x∈[x1，x2]，f(x)＋g(x)＜m(x－1)恒成立，求实数m的取值范围．
已知函数f(x)=lnx，g(x)=
(a＞0)，设F(x)=f(x)+g(x)．
（I）求函数F（x）的单调区间；
（II）若以函数y=F（x）（x∈（0，3]）的图象上任意一点P（x0，y0）为切点的切线的斜率k≤
恒成立，求实数a的最小值；
（III）是否存在实数m，使得函数y=g(
)+m-1的图象与函数y=f（1+x2）的图象恰有四个不同的交点？若存在，求出实数m的取值范围；若不存在，请说明理由．
查看习题详情和答案>>
| a |
| x |
（I）求函数F（x）的单调区间；
（II）若以函数y=F（x）（x∈（0，3]）的图象上任意一点P（x0，y0）为切点的切线的斜率k≤
| 1 |
| 3 |
（III）是否存在实数m，使得函数y=g(
| 2a |
| x2+1 |
已知函数f(x)＝lnx，
，设F(x)＝f(x)＋g(x)．
(Ⅰ)求函数F(x)的单调区间；
(Ⅱ)若以函数y＝F(x)，x∈(0，3]图像上任意一点P(x0，y0)为切点的切线的斜率k≤
恒成立，求实数a的最小值；
(Ⅲ)是否存在实数m，使得函数
的图像与函数y＝f(1＋x2)的图像恰有四个不同的交点？若存在，求出实数m的取值范围；若不存在，说明理由．
已知函数f（x）=lnx，g（x）=
（a＞0），设F（x）=f（x）+g（x）．
（Ⅰ）求F（x）的单调区间；
（Ⅱ）若以y=F（x）（x∈（0，3]）图象上任意一点P（x0，y0）为切点的切线的斜率 k≤
恒成立，求实数a的最小值．
（Ⅲ）是否存在实数m，使得函数y=g（
）+m-1的图象与y=f（1+x2）的图象恰好有四个不同的交点？若存在，求出m的取值范围，若不存在，说明理由．
查看习题详情和答案>>
| a |
| x |
（Ⅰ）求F（x）的单调区间；
（Ⅱ）若以y=F（x）（x∈（0，3]）图象上任意一点P（x0，y0）为切点的切线的斜率 k≤
| 1 |
| 2 |
（Ⅲ）是否存在实数m，使得函数y=g（
| 2a |
| x2+1 |
时，f（x）取得极小值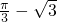
．
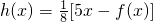，设x1是方程h（x）-x=0的实数根，若对于h（x）定义域中任意的x2、x3，当|x2-x1|＜1，且|x3-x1|＜1时，问是否存在一个最小的正整数M，使得|h（x3）-h（x2）|≤M恒成立，若存在请求出M的值；若不存在请说明理由．