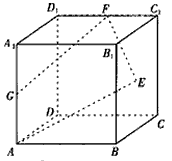
摘要: 正四面体ABCD的棱长为1.点G是底面△ABC的重心.点M在DG上.且使得∠AMB=90º.则DM的长为 .
网址:http://m.1010jiajiao.com/timu3_id_4460372[举报]
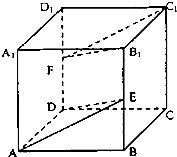 在正方体ABCD-A1B1C1D1中,棱长为1,E,F分别为棱BB1和DD1的中点.
在正方体ABCD-A1B1C1D1中,棱长为1,E,F分别为棱BB1和DD1的中点.(1)求证:平面B1FC1∥平面ADE;
(2)求四面体A1-FEA的体积.
(3)若G是C1D1上靠近C1的四等分点,动点H在底面ABCD内,且AH=
| 1 | 2 |
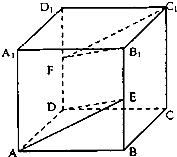
在正方体ABCD-A1B1C1D1中,棱长为1,E,F分别为棱BB1和DD1的中点.
(1)求证:平面B1FC1∥平面ADE;
(2)求四面体A1-FEA的体积.
(3)若G是C1D1上靠近C1的四等分点,动点H在底面ABCD内,且AH=
,请说明点H的轨迹,并探求GH长度的最小值.
查看习题详情和答案>>
(1)求证:平面B1FC1∥平面ADE;
(2)求四面体A1-FEA的体积.
(3)若G是C1D1上靠近C1的四等分点,动点H在底面ABCD内,且AH=
| 1 |
| 2 |

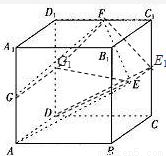
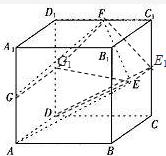 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,AA1的中点.设点E1,G1分别是点E,G在平面DCC1D1内的正投影.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,AA1的中点.设点E1,G1分别是点E,G在平面DCC1D1内的正投影.(1)求以E为顶点,以四边形FGAE在平面DCC1D1内的正投影为底面边界的棱锥的体积;
(2)证明:直线FG1⊥平面FEE1;
(3)求异面直线E1G1与EA所成角的正弦值. 查看习题详情和答案>>