摘要：已知点都在直线:y=2x+2上.为直线l与x轴的交点.数列{}是等差数列.公差为1. (1) 求数列{}与{}的通项公式, (2) 若 , 问是否存在 .若存在.求出k的值.若不存在.说明理由? (3) 求证:
网址：http://m.1010jiajiao.com/timu3_id_4459549[举报]
已知点Pn（an，bn）都在直线l：y=2x+2上，P1为直线l与x轴的交点，数列{an}成等差数列，公差为1（n∈N*）．
（I）求数列{an}，{bn}的通项公式；
（Ⅱ）若f（n）=
（m∈Z），问是否存在k∈N*，使得f（k+5）=2f（k）-2成立？若存在，求出k的值，若不存在，说明理由；
（Ⅲ）求证：
+
+…+
＜
（n≥2，n∈N*）．
查看习题详情和答案>>
（I）求数列{an}，{bn}的通项公式；
（Ⅱ）若f（n）=
|
（Ⅲ）求证：
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
已知点Pn（an，bn）都在直线L：y=2x+2上，P1为直线L与x轴的交点，数列{an}成等差数列，公差为1（n∈N*）．
（I）求数列{an}，{bn}的通项公式；
（II）求证：
＜
+
+…+
＜
（n≥3，n∈N*）．
查看习题详情和答案>>
（I）求数列{an}，{bn}的通项公式；
（II）求证：
| 1 |
| 4 |
| 1 |
| |P1P2|2 |
| 1 |
| |P1P3|2 |
| 1 |
| |P1Pn|2 |
| 2 |
| 5 |
（14分）已知点Pn(an，bn)都在直线L：y=2x+2上，P1为直线L与x轴的交点，数
列{an}成等差数列，公差为1(n∈N＊)。
（I）求数列{an}，{bn}的通项公式；
（II）求证：
(n≥3，n∈N＊)。
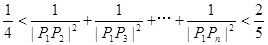(n≥3，n∈N＊)。
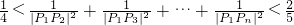（n≥3，n∈N*）．