题目内容
已知点Pn(an,bn)都在直线L:y=2x+2上,P1为直线L与x轴的交点,数列{an}成等差数列,公差为1(n∈N*).
(I)求数列{an},{bn}的通项公式;
(II)求证: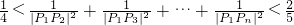 (n≥3,n∈N*).
(n≥3,n∈N*).
解:(I)∵P1为直线L:y=2x+2与x轴的交点,
∴当y=0时,x=-1,即P1(-1,0).
∴a1=-1,b1=0,
∵数列{an}成等差数列,公差为1(n∈N*),
∴an=-1+(n-1)×1=n-2,
∵点Pn(an,bn)都在直线L:y=2x+2上,
∴bn=2(n-2)+2=2n-2
(II)∵Pn(n-2,2n-2),
∴|P1Pn|= (n-1),(n≥3)
(n-1),(n≥3)
∴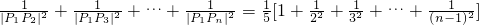
 .
.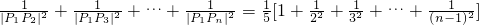 >
>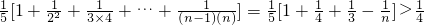 .
.
故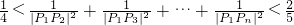 (n≥3,n∈N*).
(n≥3,n∈N*).
分析:(I)由题设知P1(-1,0),an=-1+(n-1)×1=n-2,bn=2(n-2)+2=2n-2.
(II)由Pn(n-2,2n-2),知|P1Pn|= (n-1),(n≥3),由此能够证明
(n-1),(n≥3),由此能够证明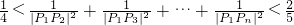 (n≥3,n∈N*).
(n≥3,n∈N*).
点评:本题考查数列的通项公式的求法和不等式的证明,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意放缩法的合理运用.
∴当y=0时,x=-1,即P1(-1,0).
∴a1=-1,b1=0,
∵数列{an}成等差数列,公差为1(n∈N*),
∴an=-1+(n-1)×1=n-2,
∵点Pn(an,bn)都在直线L:y=2x+2上,
∴bn=2(n-2)+2=2n-2
(II)∵Pn(n-2,2n-2),
∴|P1Pn|=
 (n-1),(n≥3)
(n-1),(n≥3)∴
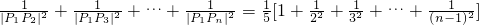
 .
.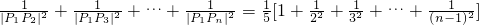 >
>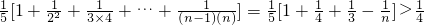 .
.故
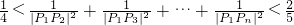 (n≥3,n∈N*).
(n≥3,n∈N*).分析:(I)由题设知P1(-1,0),an=-1+(n-1)×1=n-2,bn=2(n-2)+2=2n-2.
(II)由Pn(n-2,2n-2),知|P1Pn|=
 (n-1),(n≥3),由此能够证明
(n-1),(n≥3),由此能够证明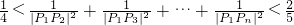 (n≥3,n∈N*).
(n≥3,n∈N*).点评:本题考查数列的通项公式的求法和不等式的证明,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意放缩法的合理运用.

练习册系列答案
相关题目