摘要： 已知f (x)＝x. (1) 证明:f (x)>0, (2) 设F(x)＝f(x+t)-f (x-t) (t≠o).试判断F(x)的奇偶性. 解:(1) 函数f (x)的定义域是{x| x∈R且x≠0}, 且f (-x)＝(-x)·＝f (x), ∴ f (x)是偶函数.当x>0时, 2x>1, 2x-1>0, ∴ f (x)>0, 当x<0时, -x>0, f (x)＝f (-x)>0, ∴ 对所有定义域内的x的值.都有f (x)>0. (2) F(-x)＝f (-x+t)-f (-x-t)＝f (x-t)-f (x+t)＝-F(x), ∴ 函数是奇函数.
网址：http://m.1010jiajiao.com/timu3_id_4459375[举报]
（本小题满分14分）已知函数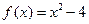
，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n ÎN *），x1＝4．
（Ⅰ）用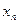
表示xn+1；
（Ⅱ）记an=lg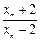
，证明数列｛an｝成等比数列，并求数列｛xn｝的通项公式；
（Ⅲ）若bn＝xn－2，试比较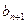
与
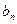的大小．
(本小题满分14分)
已知数列{an}中，a1＝t(t∈R，且t≠0,1)，a2＝t2，且当x＝t时，
函数f(x)＝(an－an－1)x2－(an＋1－an)x(n≥2，n∈N?)取得极值.
(Ⅰ)求证：数列{an＋1－an}是等比数列；
(Ⅱ)若bn＝anln|an|(n∈N?)，求数列{bn}的前n项和Sn；
(Ⅲ)当t＝－时，数列{bn}中是否存在最大项？如果存在，说明是第几项；如果不存在，请说明理由.
查看习题详情和答案>>
（本小题满分14分）已知函数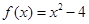
，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,0）（n Î N *），x1＝4．
（Ⅰ）用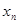
表示xn+1；
（Ⅱ）记an=lg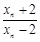
，证明数列｛an｝成等比数列，并求数列｛xn｝的通项公式；
（Ⅲ）若bn＝xn－2，试比较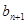
与
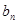的大小．
查看习题详情和答案>>
已知圆O:
交
轴于A，B两点,曲线C是以
为长轴,离心率为
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交直线X＝-2于点Q.
相切；