摘要: 如图已知F1.F2为 椭圆的两焦点.M是椭圆上一点. 延长F1M到N.P是NF2上一点.且满足 ..点N的轨迹方程为 E. ⑴求曲线E的方程, ⑵过F1的直线l交椭圆于G.交曲线E于H. .若. 求直线l的方程,
网址:http://m.1010jiajiao.com/timu3_id_4458869[举报]
(本题满分14分)
已知如图,椭圆方程为![]()
![]() .P为椭圆上的动点,
.P为椭圆上的动点,
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;
(2)已知![]() 、
、![]() ,试探究是否存在这样的点
,试探究是否存在这样的点![]() :
:![]() 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积![]() ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.
 (本题满分14分)已知如图,椭圆方程为
(本题满分14分)已知如图,椭圆方程为![]()
![]() .P为椭圆上的动点,
.P为椭圆上的动点,
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;(2)已知![]() 、
、![]() ,
,
试探究是否存在这样的点![]() :
:![]() 是轨迹T内部的整点
是轨迹T内部的整点
(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积![]() ?
?
若存在,求出点Q的坐标,若不存在,说明理由.
查看习题详情和答案>>(本题满分14分)已知如图,椭圆方程为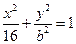
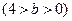 .P为椭圆上的动点,
.P为椭圆上的动点,
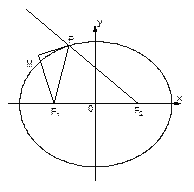
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;(2)已知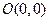 、
、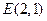 ,
,
试探究是否存在这样的点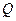 :
: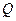 是轨迹T内部的整点
是轨迹T内部的整点
(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积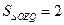 ?
?
若存在,求出点Q的坐标,若不存在,说明理由.
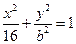
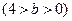 .P为椭圆上的动点,
.P为椭圆上的动点,
F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角
平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(1)求M点的轨迹T的方程;(2)已知
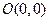 、
、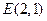 ,
,试探究是否存在这样的点
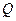 :
: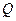 是轨迹T内部的整点
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
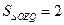 ?
?若存在,求出点Q的坐标,若不存在,说明理由.
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程.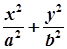 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.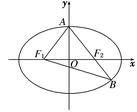
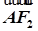 =2
=2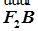 ,
,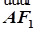 ·
·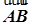 =
=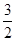 ,求椭圆的方程.
,求椭圆的方程.