Question

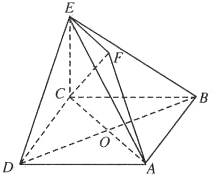如图，四边形ABCD是边长为

2

的正方形，EC⊥平面CDAB，EF∥CA，点O是AC与BD的交点，CE=EF=1．
（1）求证：AF∥平面BDE；
（2）求证：CF⊥平面BDE；
（3）求二面角A-BE-D的大小．

Answer 1

分析：（1）设AC与BD的交点为O，则DO=BO=

1

2

BD，连接EO，则可证出四边形EFAO是平行四边形，从而AF∥EO，由线面平行的判定定理，可得AF∥平面BDE；
（2）连接FO，可证明四边形CEFO是正方形，可得对角线CF⊥EO．可证ED=EB又OD=OB，所以EO⊥BD，从而可证明CF⊥平面BDE．也可以建立空间直角坐标系，利用两直线垂直与两条直线的方向向量的数量积为零的关系来证明．
（3）通过可以建立空间直角坐标系，先求出二面角的两半平面的法向量的夹角，进而即可求出二面角的平面角．

解答：解：（1）连接EO，∵正方形ABCD的边长为

2

，∴其对角线AC=2．
∵EF∥CO，且EF=1，AO=

1

2

AC=1，
∴四边形AOEF为平行四边形，∴AF∥OE．
又∵EO?平面BDE，AF?平面BDE，∴AF∥平面BDE．
（2）证法一：连接OF，∵EC⊥平面ABCD，∴EC⊥CO，EC⊥CD，EC⊥DB．
又∵EF∥CO，CE=EF=CO=1，∴四边形CEFO是正方形，∴CF⊥EO．
又∵CD=CB=

2

，∴DE=BE．
∵O是BD的中点，∴EO⊥BD．
∵EC∩EO=E，∴DB⊥平面CEFO，∴DB⊥CF．
而EO∩BD=O，∴CF⊥平面BDE．
证法二：由已知条件建立如图所示的空间直角坐标系C-xyz，
可知C（0，0，0），A（

2

，

2

，0），B（0，

2

，0），D（

2

，0，0），E（0，0，1），F(

2

2

，

2

2

，1)．
∴

CF

=(

2

2

，

2

2

，1)，

BE

=(0，-

2

，1)，

DE

=(-

2

，0，1)．
∵

CF

•

BE

=0-1+1=0，∴CF⊥BE；
∵

CF

•

DE

=-1+0+1=0，∴CF⊥DE．
∵BE∩DE=E，∴CF⊥平面BDE．
（3）设平面BDE的法向量为

n1

=(x1，y1，z1)，∴

n1

•

BE

=0，

n1

•

DE

=0，
得

- 2 y1+z1=0 - 2 x1+z1=0

，令z1=

2

，则y₁=1，x₁=1，∴

n1

=(1，1，

2

)．
设平面ABE的法向量

n2

=(x2，y2，z2)，∵

AE

=(-

2

，-

2

，1)，

AB

=(-

2

，0，0)，
∴

n2

•

AE

=-

2

x2-

2

y2+z2=0，

n2

•

AB

=-

2

x2=0．
∴x₂=0．令z2=

2

，则y₂=1，∴

n2

=(0，1，

2

)．
∴cos＜

n1

，

n2

＞=

n1 • n2

| n1 || n2 |

=

0+1+2

4 × 3

=

3

2

．∴＜

n1

，

n2

＞=

π

6

．
由图可知二面角A-BE-D的平面角为

π

6

．

点评：本题综合考查了线面的平行、垂直及二面角的平面角，熟练掌握判定定理和性质定理及通过建立空间直角坐标系利用数量积等于0与垂直的关系是解题的关键．