摘要： 已知函数.对任意实数x.y分别满足 ① ②为正整数 (1)求数列.的通项公式, (2)设的前n项和.
网址：http://m.1010jiajiao.com/timu3_id_4458354[举报]
(理)对任意实数x、y,函数f(x)、g(x)满足f(x+1)=
f(x),且f(0)=3,g(x+y)=g(x)+2y,g(5)=13,n∈N*.
f(x),且f(0)=3,g(x+y)=g(x)+2y,g(5)=13,n∈N*.(1)求{f(n)}、{g(n)}的通项公式;
(2)设cn=g［
f(n)］,求数列{cn}的前n项和;
(3)已知
=0,设F(n)=Sn-3n,是否存在整数m和M,使得对任意正整数n,不等式m＜F(n)＜M恒成立?若存在,分别求出m和M的集合,并求出M-m的最小值;若不存在,请说明理由.
(文)已知f(x)=
x3-3x,g(x)=2ax2.
(1)当-
≤a≤
时,求证:F(x)=f(x)-g(x)在(-1,1)上是单调函数;
(2)若g′(x)≤
〔g′(x)为g(x)的导函数〕在［-1,
］上恒成立,求a的取值范围.
已知函数f（x）=ax2+lnx（x＞0），g（x）=2x（x∈R），函数h（x）=f（x）-g（x）在区间（0，+∞）上为增函数．
（1）求实数a的取值范围；
（2）设f′（x）、h′（x）分别是f（x）、h（x）的导函数，若方程h′（x）=0在区间（0，+∞）上有唯一解，
①令函数mn（x）=[f′（x）]n-f（xn+
），其中n∈N*且n≥2.2函数y=mn（x）在区间（0，+∞）上的最小值；
②求证：对任意的正实数x，都有
＜
．
查看习题详情和答案>>
（1）求实数a的取值范围；
（2）设f′（x）、h′（x）分别是f（x）、h（x）的导函数，若方程h′（x）=0在区间（0，+∞）上有唯一解，
①令函数mn（x）=[f′（x）]n-f（xn+
| 1 |
| xn |
②求证：对任意的正实数x，都有
| n |
 |
| i=2 |
| 1 |
| mi(x) |
| 5 |
| 6 |
已知函数f(x)=x+
(t＞0)和点P（1，0），过点P作曲线y=f（x）的两条切线PM、PN，切点分别为M、N．
（Ⅰ）设|MN|=g（t），试求函数g（t）的表达式；
（Ⅱ）是否存在t，使得M、N与A（0，1）三点共线．若存在，求出t的值；若不存在，请说明理由．
（Ⅲ）在（Ⅰ）的条件下，若对任意的正整数n，在区间[2，n+
]内总存在m+1个实数a1，a2，…，am，am+1，使得不等式g（a1）+g（a2）+…+g（am）＜g（am+1）成立，求m的最大值．
查看习题详情和答案>>
| t |
| x |
（Ⅰ）设|MN|=g（t），试求函数g（t）的表达式；
（Ⅱ）是否存在t，使得M、N与A（0，1）三点共线．若存在，求出t的值；若不存在，请说明理由．
（Ⅲ）在（Ⅰ）的条件下，若对任意的正整数n，在区间[2，n+
| 64 |
| n |
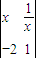（x＞0）的值域为集合A，
]，不等式f（x）+a≥0恒成立，求实数a的范围；
•
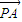的值．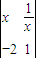
（x＞0）的值域为集合A，
]，不等式f（x）+a≥0恒成立，求实数a的范围；
•
的值．