题目内容
已知函数f(x)=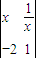 (x>0)的值域为集合A,
(x>0)的值域为集合A,(1)若全集U=R,求CUA;
(2)对任意x∈(0,
 ],不等式f(x)+a≥0恒成立,求实数a的范围;
],不等式f(x)+a≥0恒成立,求实数a的范围;(3)设P是函数f(x)的图象上任意一点,过点P分别向直线y=x和y轴作垂线,垂足分别为A、B,求
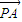 •
•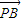 的值.
的值.
【答案】分析:(1)根据二阶矩阵运算的法则化得f(x)的解析式,再利用基本不等式得集合A,由补集的含义即可写出答案;
(2)由题得a≥-(x+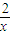 ),只须求出a大于等于函数y=-(x+
),只须求出a大于等于函数y=-(x+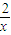 )在(0,
)在(0, ]的最大值,再利用函数的单调性得出函数y=-(x+
]的最大值,再利用函数的单调性得出函数y=-(x+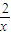 )在(0,
)在(0, ]的最大值,即可实数a的范围;
]的最大值,即可实数a的范围;
(3)先设P(x,x+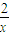 ),写出直线PA的方程,再与直线y=x的方程联立,得A点的坐标,最后利用向量数量积的坐标运算计算即得答案.
),写出直线PA的方程,再与直线y=x的方程联立,得A点的坐标,最后利用向量数量积的坐标运算计算即得答案.
解答:解:(1)由已知得,x>0,则f(x)=x+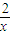 ≥2
≥2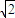 …(1分)
…(1分)
当且仅当x=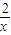 时,即x=
时,即x=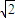 等号成立,
等号成立,
∴A=[2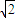 ,+∞) …(3分)
,+∞) …(3分)
所以,CUA=(-∞,2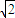 ) …(4分)
) …(4分)
(2)由题得 a≥-(x+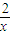 ) …(5分)
) …(5分)
函数y=-(x+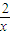 )在(0,
)在(0, ]的最大值为-
]的最大值为- …(9分)
…(9分)
∴a≥- …(10分)
…(10分)
(3)设P(x,x+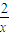 ),则直线PA的方程为
),则直线PA的方程为
y-(x+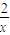 )=-(x-x),
)=-(x-x),
即y=-x+2x+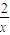 …(11分)
…(11分)
由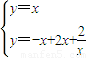 得A(x+
得A(x+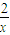 ,2x+
,2x+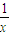 ) …(13分)
) …(13分)
又B(0,x+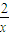 ),…(14分)
),…(14分)
所以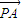 =(
=(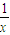 ,-
,-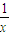 ),
),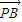 =(-x,0),
=(-x,0),
故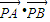 =
= (-x)=-1 …(16分)
(-x)=-1 …(16分)
点评:本题考查二阶矩阵、补集的含义、平面向量数量积的运算等,考查运算能力,属于基础题.
(2)由题得a≥-(x+
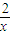 ),只须求出a大于等于函数y=-(x+
),只须求出a大于等于函数y=-(x+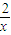 )在(0,
)在(0, ]的最大值,再利用函数的单调性得出函数y=-(x+
]的最大值,再利用函数的单调性得出函数y=-(x+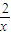 )在(0,
)在(0, ]的最大值,即可实数a的范围;
]的最大值,即可实数a的范围;(3)先设P(x,x+
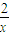 ),写出直线PA的方程,再与直线y=x的方程联立,得A点的坐标,最后利用向量数量积的坐标运算计算即得答案.
),写出直线PA的方程,再与直线y=x的方程联立,得A点的坐标,最后利用向量数量积的坐标运算计算即得答案.解答:解:(1)由已知得,x>0,则f(x)=x+
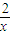 ≥2
≥2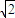 …(1分)
…(1分)当且仅当x=
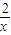 时,即x=
时,即x=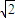 等号成立,
等号成立,∴A=[2
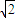 ,+∞) …(3分)
,+∞) …(3分)所以,CUA=(-∞,2
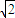 ) …(4分)
) …(4分)(2)由题得 a≥-(x+
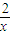 ) …(5分)
) …(5分)函数y=-(x+
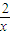 )在(0,
)在(0, ]的最大值为-
]的最大值为- …(9分)
…(9分)∴a≥-
 …(10分)
…(10分)(3)设P(x,x+
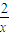 ),则直线PA的方程为
),则直线PA的方程为y-(x+
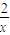 )=-(x-x),
)=-(x-x),即y=-x+2x+
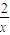 …(11分)
…(11分)由
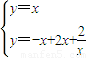 得A(x+
得A(x+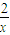 ,2x+
,2x+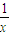 ) …(13分)
) …(13分)又B(0,x+
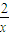 ),…(14分)
),…(14分)所以
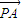 =(
=(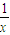 ,-
,-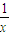 ),
),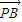 =(-x,0),
=(-x,0),故
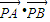 =
= (-x)=-1 …(16分)
(-x)=-1 …(16分)点评:本题考查二阶矩阵、补集的含义、平面向量数量积的运算等,考查运算能力,属于基础题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|