集合A是由具备下列性质的函数f（x）组成的：
①函数f（x）的定义域是[0，+∞）；
②函数f（x）的值域是[-2，4）；
③函数f（x）在[0，+∞）上是增函数，分别探究下列小题：
（1）判断函数f₁（x）=

x

-2（x≥0）及f₂（x）=4-6•（

1

2

）^x（x≥0）是否属于集合A？并简要说明理由；
（2）对于（1）中你认为属于集合A的函数f（x），不等式f（x）+f（x+2）＜2f（x+1）是否对于任意的x≥0恒成立？若不成立，为什么？若成立，请说明你的结论．
（3）g（x）=x+2a f₁（x）求g（x）的最小值用a表示．

集合A是由适合以下性质的函数f（x）构成的：对于定义域内任意两个不相等的实数x₁，x₂，都有

1

2

[f(x1)+f(x2)]＞f(

x1+x2

2

)．
（1）试判断f（x）=x²及g（x）=log₂x是否在集合A中，并说明理由；
（2）设f（x）∈A且定义域为（0，+∞），值域为（0，1），f(1)＞

1

2

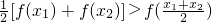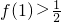，试求出一个满足以上条件的函数f （x）的解析式．

集合A是以适合以下性质的函数f(x)构成的：对于定义域内任意两个不相等的实数x₁，x₂，都有；
（1）判断f(x)=x²及g(x)=log₂x是否在集合A中，请说明理由；
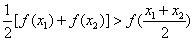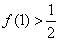（2）设f(x)∈A，且定义域为(0，+∞)，值域为(0，1)，，试求出一个满足以上条件的一个函数f(x)的解析式。