题目内容
集合A是由适合以下性质的函数f（x）构成的：对于定义域内任意两个不相等的实数x1，x2，都有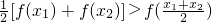
．
（1）试判断f（x）=x2及g（x）=log2x是否在集合A中，并说明理由；
（2）设f（x）∈A且定义域为（0，+∞），值域为（0，1），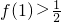
，试求出一个满足以上条件的函数f （x）的解析式．
解：（1）f（x）∈A，g（x）∉A．（2分）
对于f（x）∈A的证明．任意x1，x2∈R且x1≠x2，
=
即
．∴f（x）∈A（3分）
对于g（x）∉A，举反例：当x1=1，x2=2时，
，
，
不满足
．∴g（x）∉A．（4分）
（2）函数
，当x∈（0，+∞）时，
值域为（0，1）且
．（6分）
任取x1，x2∈（0，+∞）且x1≠x2，
则
=
即．
∴
．是一个符合条件的函数．（8分）
分析：（1）f（x）∈A，g（x）∉A．对于f（x）∈A的证明只要看是否满足条件即可，用作差法进行验证．g（x）∉A，可通过举反例来证明，如取x1=1，x2=2，不满足．
（2）受（1）的启发，可从指数函数中去找，先按照条件“当x∈（0，+∞）时，
值域为（0，1）且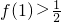”找到，再证明是否满足条件条件即可．
点评：本题是一道情境题，主要考查不等式的证明以及不等式的应用，还考查了构造思想，如本题中f（x）构造类型f（x）=ax
或
（k＞1）很常见．
对于f（x）∈A的证明．任意x1，x2∈R且x1≠x2，
=
即
．∴f（x）∈A（3分）对于g（x）∉A，举反例：当x1=1，x2=2时，
，，不满足
．∴g（x）∉A．（4分）（2）函数
，当x∈（0，+∞）时，值域为（0，1）且
．（6分）任取x1，x2∈（0，+∞）且x1≠x2，
则
=
即
．∴
．是一个符合条件的函数．（8分）分析：（1）f（x）∈A，g（x）∉A．对于f（x）∈A的证明只要看是否满足条件
即可，用作差法进行验证．g（x）∉A，可通过举反例来证明，如取x1=1，x2=2，不满足．（2）受（1）的启发，可从指数函数中去找，先按照条件“当x∈（0，+∞）时，
值域为（0，1）且
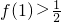”找到，再证明是否满足条件条件即可．点评：本题是一道情境题，主要考查不等式的证明以及不等式的应用，还考查了构造思想，如本题中f（x）构造类型f（x）=ax
或（k＞1）很常见． 
练习册系列答案
相关题目