题目内容
(A类)已知函数g(x)=(a+1)x-2+1(a>0)的图象恒过定点A,且点A又在函数f(x)=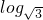 (x+a)的图象上.
(x+a)的图象上.
(1)求实数a的值; (2)解不等式f(x)<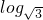 a;
a;
(3)|g(x+2)-2|=2b有两个不等实根时,求b的取值范围.
(B类)设f(x)是定义在R上的函数,对任意x,y∈R,恒有f(x+y)=f(x)+f(y)
(1)求f(0)的值; (2)求证:f(x)为奇函数;
(3)若函数f(x)是R上的增函数,已知f(1)=1,且f(2a)>f(a-1)+2,求a的取值范围.
A类:解:(1)∵函数g(x)=(a+1)x-2+1(a>0)的图象恒过定点A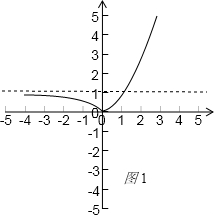
∴A点的坐标为(2,2)
又因为A点在f(x)=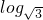 (x+a)的图象上,
(x+a)的图象上,
∴2=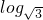 (2+a)
(2+a)
即a+2=3
∴a=1
(2)∵不等式f(x)<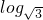 a?
a?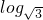 (x+1)<
(x+1)<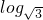 1=0
1=0
?0<x+1<1
?-1<x<0
∴不等式f(x)<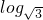 a的解集为(-1,0)
a的解集为(-1,0)
(3)∵g(x)=2x-2+1
∴g(x+2)=2x+1
∴|g(x+2)-2|=2b?|2x+1-2|=2b?|2x-1|=2b
函数y=|2x-1|的图象如图1,
要使|g(x+2)-2|=2b有两个不等实根
由图象可知需0<2b<1,
故b的取值范围为(0, )
)
B类:解:(1)令x=y=0
则f(0)=f(0)+f(0)
∴f(0)=0
(2)令y=-x
则f(0)=f(x)+f(-x)
∴f(-x)=-f(x)
所以f(x)为R上的奇函数
(3)令x=y=1
则f(1+1)=f(2)=f(1)+f(1)=2
∴f(2)=2
∴f(2a)>f(a-1)+2?f(2a)>f(a-1)+f(2)?f(2a)>f(a+1)
又∵f(x)是R上的增函数,所以2a>a+1
即a>1
∴a的取值范围为(1,+∞)
分析:(A类)(1)利用指数函数的图象和性质即可得函数g(x)所过定点,代入函数f(x)的解析式即可求得a的值,(2)利用对数函数的定义和单调性解不等式即可,(3)将方程等价转化为|2x-1|=2b,画出函数y=|2x-1|的图象,数形结合即可得b的范围
(B类)(1)利用赋值法,令x=y=0,即可得f(0),(2)利用赋值法和奇函数定义,令y=-x,即可证明,(3)先计算出f(2)=2,再将不等式等价转化为f(2a)>f(a+1),最后利用单调性解不等式即可
点评:本题综合考查了指数函数的图象和性质,对数函数的图象和性质,抽象表达式的意义,利用函数图象和单调性解不等式等

∴A点的坐标为(2,2)
又因为A点在f(x)=
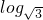 (x+a)的图象上,
(x+a)的图象上,∴2=
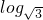 (2+a)
(2+a)即a+2=3
∴a=1
(2)∵不等式f(x)<
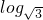 a?
a?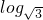 (x+1)<
(x+1)<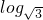 1=0
1=0?0<x+1<1
?-1<x<0
∴不等式f(x)<
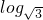 a的解集为(-1,0)
a的解集为(-1,0)(3)∵g(x)=2x-2+1
∴g(x+2)=2x+1
∴|g(x+2)-2|=2b?|2x+1-2|=2b?|2x-1|=2b
函数y=|2x-1|的图象如图1,
要使|g(x+2)-2|=2b有两个不等实根
由图象可知需0<2b<1,
故b的取值范围为(0,
 )
) B类:解:(1)令x=y=0
则f(0)=f(0)+f(0)
∴f(0)=0
(2)令y=-x
则f(0)=f(x)+f(-x)
∴f(-x)=-f(x)
所以f(x)为R上的奇函数
(3)令x=y=1
则f(1+1)=f(2)=f(1)+f(1)=2
∴f(2)=2
∴f(2a)>f(a-1)+2?f(2a)>f(a-1)+f(2)?f(2a)>f(a+1)
又∵f(x)是R上的增函数,所以2a>a+1
即a>1
∴a的取值范围为(1,+∞)
分析:(A类)(1)利用指数函数的图象和性质即可得函数g(x)所过定点,代入函数f(x)的解析式即可求得a的值,(2)利用对数函数的定义和单调性解不等式即可,(3)将方程等价转化为|2x-1|=2b,画出函数y=|2x-1|的图象,数形结合即可得b的范围
(B类)(1)利用赋值法,令x=y=0,即可得f(0),(2)利用赋值法和奇函数定义,令y=-x,即可证明,(3)先计算出f(2)=2,再将不等式等价转化为f(2a)>f(a+1),最后利用单调性解不等式即可
点评:本题综合考查了指数函数的图象和性质,对数函数的图象和性质,抽象表达式的意义,利用函数图象和单调性解不等式等

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目