摘要:设函数的定义域为R.当x<0时>1.且对任意的实数x.y∈R.有 (Ⅰ)求,判断并证明函数的单调性, (Ⅱ)数列满足,且 ①求通项公式. ②当时.不等式对不小于2的正整数恒成立.求x的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_4455903[举报]
设函数f(x)的定义域为R,当x<0时f(x)>1,且对任意的实数x,y∈R,有![]()
(Ⅰ)求f(0),判断并证明函数f(x)的单调性;
(Ⅱ)数列![]() 满足
满足![]() ,且
,且![]() ,数列
,数列![]() 满足
满足![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
①求数列![]() 通项公式。
通项公式。
②求数列![]() 的前n项和Tn的最小值及相应的n的值.
的前n项和Tn的最小值及相应的n的值.
已知函数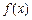 的定义域为R,其导数
的定义域为R,其导数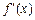 满足0<
满足0<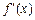 <1.设a是方程
<1.设a是方程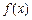 =x的根.
=x的根.
(Ⅰ)当x>a时,求证: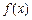 <x;
<x;
(Ⅱ)求证:|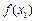 -
-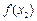 |<|x1-x2|(x1,x2∈R,x1≠x2);
|<|x1-x2|(x1,x2∈R,x1≠x2);
(Ⅲ)试举一个定义域为R的函数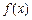 ,满足0<
,满足0<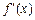 <1,且
<1,且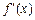 不为常数.
不为常数.
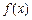 的定义域为R,其导数
的定义域为R,其导数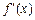 满足0<
满足0<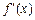 <1.设a是方程
<1.设a是方程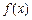 =x的根.
=x的根.(Ⅰ)当x>a时,求证:
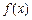 <x;
<x;(Ⅱ)求证:|
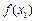 -
-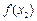 |<|x1-x2|(x1,x2∈R,x1≠x2);
|<|x1-x2|(x1,x2∈R,x1≠x2);(Ⅲ)试举一个定义域为R的函数
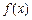 ,满足0<
,满足0<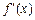 <1,且
<1,且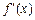 不为常数.
不为常数.
设函数f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y∈R,有f(x+y)=f(x)·f(y)成立,数列{an}满足a1=f(0)且f(an+1)=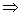 (n∈N*)
(n∈N*)
(1)求a2 007;
(2)若不等式(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() )≥k·
)≥k·![]() 对一切n∈N*均成立,求k的最大值.
对一切n∈N*均成立,求k的最大值.